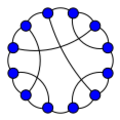
Frucht graph
| Frucht graph | |
|---|---|
| File:200px The Frucht graph | |
| Named after | Robert Frucht |
| Vertices | 12 |
| Edges | 18 |
| Radius | 3 |
| Diameter | 4 |
| Girth | 3 |
| Automorphisms | 1 ({id}) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Cubic Halin Pancyclic |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Frucht graph is a cubic graph with 12 vertices, 18 edges, and no nontrivial symmetries.[1] It was first described by Robert Frucht in 1949.[2]
The Frucht graph can be constructed from the LCF notation: [−5,−2,−4,2,5,−2,2,5,−2,−5,4,2].
Properties
The Frucht graph is one of the five smallest cubic graphs possessing only a single graph automorphism, the identity: every vertex can be distinguished topologically from every other vertex.[3] Such graphs are called asymmetric (or identity) graphs. Frucht's theorem states that any finite group can be realized as the group of symmetries of a graph,[4] and a strengthening of this theorem, also due to Frucht, states that any finite group can be realized as the symmetries of a 3-regular graph.[2] The Frucht graph provides an example of this strengthened realization for the trivial group.
The characteristic polynomial of the Frucht graph is .
The Frucht graph is a pancyclic, Halin graph with chromatic number 3, chromatic index 3, radius 3, and diameter 4. Like every Halin graph, the Frucht graph is polyhedral (planar and 3-vertex-connected)[5] and Hamiltonian, with girth 3. Its independence number is 5.
Gallery
-
The chromatic number of the Frucht graph is 3.
-
The Frucht graph is Hamiltonian.
References
- ↑ Weisstein, Eric W.. "Frucht Graph". http://mathworld.wolfram.com/FruchtGraph.html.
- ↑ 2.0 2.1 Frucht, R. (1949), "Graphs of degree three with a given abstract group", Canadian Journal of Mathematics 1 (4): 365–378, doi:10.4153/CJM-1949-033-6, ISSN 0008-414X
- ↑ Bussemaker, F. C.; Cobeljic, S.; Cvetkovic, D. M.; Seidel, J. J. (1976), Computer investigation of cubic graphs, EUT report, 76-WSK-01, Department of Mathematics and Computing Science, Eindhoven University of Technology, https://research.tue.nl/en/publications/computer-investigation-of-cubic-graphs
- ↑ Frucht, R. (1939), "Herstellung von Graphen mit vorgegebener abstrakter Gruppe." (in German), Compositio Mathematica 6: 239–250, ISSN 0010-437X, http://www.numdam.org/item?id=CM_1939__6__239_0
- ↑ Weisstein, Eric W.. "Halin Graph". http://mathworld.wolfram.com/HalinGraph.html.
 |