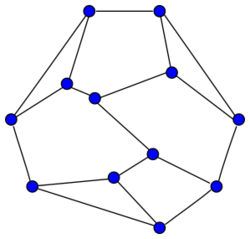
Asymmetric graph

Short description: Undirected graph with no non-trivial symmetries

The eight 6-vertex asymmetric graphs

The Frucht graph, one of the five smallest asymmetric cubic graphs.

Graph families defined by their automorphisms
distance-transitive	→	distance-regular	←	strongly regular
↓
symmetric (arc-transitive)	←	t-transitive, t ≥ 2		skew-symmetric
↓
(if connected) vertex- and edge-transitive	→	edge-transitive and regular	→	edge-transitive
↓		↓		↓
vertex-transitive	→	regular	→	(if bipartite) biregular
↑
Cayley graph	←	zero-symmetric		asymmetric

In graph theory, a branch of mathematics, an undirected graph is called an asymmetric graph if it has no nontrivial symmetries.

Formally, an automorphism of a graph is a permutation p of its vertices with the property that any two vertices u and v are adjacent if and only if p(u) and p(v) are adjacent. The identity mapping of a graph onto itself is always an automorphism, and is called the trivial automorphism of the graph. An asymmetric graph is a graph for which there are no other automorphisms.

Note that the term "asymmetric graph" is not a negation of the term "symmetric graph," as the latter refers to a stronger condition than possessing nontrivial symmetries.

Examples

The smallest asymmetric non-trivial graphs have 6 vertices. The smallest asymmetric regular graphs have ten vertices; there exist ten-vertex asymmetric graphs that are 4-regular and 5-regular.

Trees

The smallest asymmetric tree has seven vertices: it consists of three paths of lengths 1, 2, and 3, linked at a common endpoint. In contrast to the situation for graphs, almost all trees are symmetric. In particular, if a tree is chosen uniformly at random among all trees on n labeled nodes, then with probability tending to 1 as n increases, the tree will contain some two leaves adjacent to the same node and will have symmetries exchanging these two leaves.