Fuhrmann triangle

Fuhrmann triangle (red): [math]\displaystyle{ \triangle M^\prime_c M^\prime_b M^\prime_a }[/math]
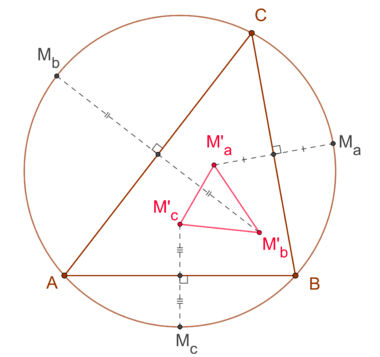
mid arc points: [math]\displaystyle{ M_a, M_b, M_c }[/math]

Fuhrmann triangle (red): [math]\displaystyle{ \triangle M^\prime_c M^\prime_b M^\prime_a }[/math]
[math]\displaystyle{ \triangle M^\prime_c M^\prime_b M^\prime_a \sim \triangle M_a M_b M_c }[/math]

The Fuhrmann triangle, named after Wilhelm Fuhrmann (1833–1904), is special triangle based on a given arbitrary triangle.

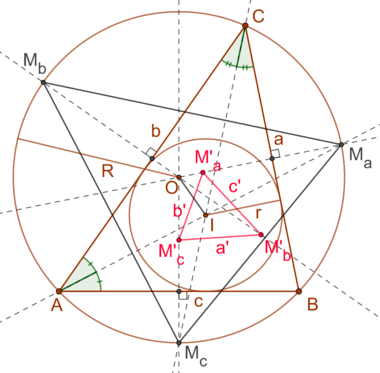
For a given triangle [math]\displaystyle{ \triangle ABC }[/math] and its circumcircle the midpoints of the arcs over triangle sides are denoted by [math]\displaystyle{ M_a, M_b, M_c }[/math]. Those midpoints get reflected at the associated triangle sides yielding the points [math]\displaystyle{ M^\prime_a, M^\prime_b, M^\prime_c }[/math], which forms the Fuhrmann triangle.

The circumcircle of Fuhrmann triangle is the Fuhrmann circle. Furthermore the Furhmann triangle is similar to the triangle formed by the mid arc points, that is [math]\displaystyle{ \triangle M^\prime_c M^\prime_b M^\prime_a \sim \triangle M_a M_b M_c }[/math]. For the area of the Fuhrmann triangle the following formula holds:

[math]\displaystyle{ |\triangle M^\prime_c M^\prime_b M^\prime_a| = \frac{(a+b+c)|OI|^2}{4R}=\frac{(a+b+c)(R-2r)}{4} }[/math]

Where [math]\displaystyle{ O }[/math] denotes the circumcenter of the given triangle [math]\displaystyle{ \triangle ABC }[/math] and [math]\displaystyle{ R }[/math] its radius as well as [math]\displaystyle{ I }[/math] denoting the incenter and [math]\displaystyle{ r }[/math] its radius. Due to Euler's theorem one also has [math]\displaystyle{ |OI|^2=R(R-2r) }[/math]. The following equations hold for the sides of the Fuhrmann triangle:

[math]\displaystyle{ a^\prime=\sqrt{\frac{(-a+b+c)(a+b+c)}{bc}}|OI| }[/math]

[math]\displaystyle{ b^\prime=\sqrt{\frac{(a-b+c)(a+b+c)}{ac}}|OI| }[/math]

[math]\displaystyle{ c^\prime=\sqrt{\frac{(a+b-c)(a+b+c)}{ab}}|OI| }[/math]

Where [math]\displaystyle{ a, b, c }[/math] denote the sides of the given triangle [math]\displaystyle{ \triangle ABC }[/math] and [math]\displaystyle{ a^\prime, b^\prime, c^\prime }[/math] the sides of the Fuhrmann triangle (see drawing).