Fuhrmann circle
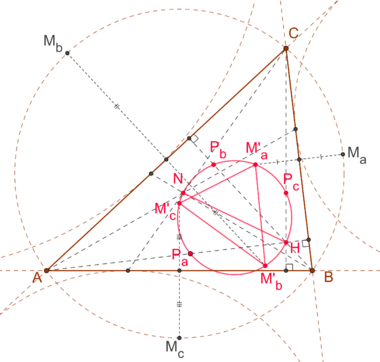
In geometry, the Fuhrmann circle of a triangle, named after the German Wilhelm Fuhrmann (1833–1904), is the circle with a diameter of the line segment between the orthocenter [math]\displaystyle{ H }[/math] and the Nagel point [math]\displaystyle{ N }[/math]. This circle is identical with the circumcircle of the Fuhrmann triangle.[1]
The radius of the Fuhrmann circle of a triangle with sides a, b, and c and circumradius R is
- [math]\displaystyle{ R\sqrt{\frac{a^3-a^2b-ab^2+b^3-a^2c+3abc-b^2c-ac^2+c^3}{abc}}, }[/math]
which is also the distance between the circumcenter and incenter.[2]
Aside from the orthocenter the Fuhrmann circle intersects each altitude of the triangle in one additional point. Those points all have the distance [math]\displaystyle{ 2r }[/math] from their associated vertices of the triangle. Here [math]\displaystyle{ r }[/math] denotes the radius of the triangles incircle.[3]
Notes
- ↑ Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN:978-0-486-46237-0, pp. 228–229, 300 (originally published 1929 with Houghton Mifflin Company (Boston) as Modern Geometry).
- ↑ Weisstein, Eric W.. "Fuhrmann Circle". http://mathworld.wolfram.com/FuhrmannCircle.html.
- ↑ Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. MAA, 1995, pp. 49-52
Further reading
- Nguyen Thanh Dung: "The Feuerbach Point and the Fuhrmann Triangle". Forum Geometricorum, Volume 16 (2016), pp. 299–311.
- J. A. Scott: An Eight-Point Circle. In: The Mathematical Gazette, Volume 86, No. 506 (Jul., 2002), pp. 326–328 (JSTOR)
External links