Gauss–Hermite quadrature
In numerical analysis, Gauss–Hermite quadrature is a form of Gaussian quadrature for approximating the value of integrals of the following kind:
- [math]\displaystyle{ \int_{-\infty}^{+\infty} e^{-x^2} f(x)\,dx. }[/math]
In this case
- [math]\displaystyle{ \int_{-\infty}^{+\infty} e^{-x^2} f(x)\,dx \approx \sum_{i=1}^n w_i f(x_i) }[/math]
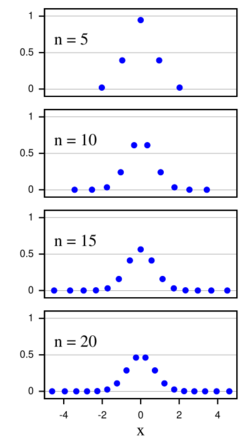
where n is the number of sample points used. The xi are the roots of the physicists' version of the Hermite polynomial Hn(x) (i = 1,2,...,n), and the associated weights wi are given by [1]
- [math]\displaystyle{ w_i = \frac {2^{n-1} n! \sqrt{\pi}} {n^2[H_{n-1}(x_i)]^2}. }[/math]
Example with change of variable
Consider a function h(y), where the variable y is Normally distributed: [math]\displaystyle{ y \sim \mathcal{N}(\mu,\sigma^2) }[/math]. The expectation of h corresponds to the following integral:
[math]\displaystyle{ E[h(y)] = \int_{-\infty}^{+\infty} \frac{1}{\sigma \sqrt{2\pi}} \exp \left( -\frac{(y-\mu)^2}{2\sigma^2} \right) h(y) dy }[/math]
As this does not exactly correspond to the Hermite polynomial, we need to change variables:
[math]\displaystyle{ x = \frac{y-\mu}{\sqrt{2} \sigma} \Leftrightarrow y = \sqrt{2} \sigma x + \mu }[/math]
Coupled with the integration by substitution, we obtain:
[math]\displaystyle{ E[h(y)] = \int_{-\infty}^{+\infty} \frac{1}{\sqrt{\pi}} \exp(-x^2) h(\sqrt{2} \sigma x + \mu) dx }[/math]
leading to:
[math]\displaystyle{ E[h(y)] \approx \frac{1}{\sqrt{\pi}} \sum_{i=1}^n w_i h(\sqrt{2} \sigma x_i + \mu) }[/math]
References
- ↑ Abramowitz, M & Stegun, I A, Handbook of Mathematical Functions, 10th printing with corrections (1972), Dover, ISBN:978-0-486-61272-0. Equation 25.4.46.
- Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., eds. (2010), "Quadrature: Gauss–Hermite Formula", NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, http://dlmf.nist.gov/3.5.E28
- Shao, T. S.; Chen, T. C.; Frank, R. M. (1964). "Tables of zeros and Gaussian weights of certain associated Laguerre polynomials and the related generalized Hermite polynomials". Math. Comp. 18 (88): 598–616. doi:10.1090/S0025-5718-1964-0166397-1.
- Steen, N. M.; Byrne, G. D.; Gelbard, E. M. (1969). "Gaussian quadratures for the integrals [math]\displaystyle{ \textstyle\int_0^\infty e^{-x^2} f(x) dx }[/math] and [math]\displaystyle{ \textstyle\int_0^b e^{-x^2} f(x) dx }[/math]". Math. Comp. 23 (107): 661–671. doi:10.1090/S0025-5718-1969-0247744-3.
- Shizgal, B. (1981). "A Gaussian quadrature procedure for use in the solution of the Boltzmann equation and related problems". J. Comput. Phys. 41: 309–328. doi:10.1016/0021-9991(81)90099-1.
External links
- For tables of Gauss-Hermite abscissae and weights up to order n = 32 see http://www.efunda.com/math/num_integration/findgausshermite.cfm.
- Generalized Gauss–Hermite quadrature, free software in C++, Fortran, and Matlab
 |