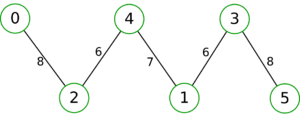
Gomory–Hu tree

From HandWiki
Short description: Weighted tree representing s-t cuts of a graph

In combinatorial optimization, the Gomory–Hu tree[1] of an undirected graph with capacities is a weighted tree that represents the minimum s-t cuts for all s-t pairs in the graph. The Gomory–Hu tree can be constructed in |V| − 1 maximum flow computations. It is named for Ralph E. Gomory and T. C. Hu.

Definition

Let [math]\displaystyle{ G = (V_G, E_G, c) }[/math] be an undirected graph with [math]\displaystyle{ c(u,v) }[/math] being the capacity of the edge [math]\displaystyle{ (u,v) }[/math] respectively.

Denote the minimum capacity of an s-t cut by [math]\displaystyle{ \lambda_{st} }[/math] for each [math]\displaystyle{ s, t \in V_G }[/math].
Let [math]\displaystyle{ T = (V_G, E_T) }[/math] be a tree, and denote the set of edges in an s-t path by [math]\displaystyle{ P_{st} }[/math] for each [math]\displaystyle{ s,t \in V_G }[/math].

Then T is said to be a Gomory–Hu tree of G, if for each [math]\displaystyle{ s, t \in V_G }[/math]

[math]\displaystyle{ \lambda_{st} = \min_{e\in P_{st}} c(S_e, T_e), }[/math]

where

  1. [math]\displaystyle{ S_e, T_e \subseteq V_G }[/math] are the two connected components of [math]\displaystyle{ T \setminus \{e\} }[/math], and thus [math]\displaystyle{ (S_e, T_e) }[/math] forms an s-t cut in G.
  2. [math]\displaystyle{ c(S_e, T_e) }[/math] is the capacity of the [math]\displaystyle{ (S_e,T_e) }[/math] cut in G.

Algorithm

Gomory–Hu Algorithm

Input: A weighted undirected graph [math]\displaystyle{ G = ((V_G,E_G), c) }[/math]
Output: A Gomory–Hu Tree [math]\displaystyle{ T = (V_T, E_T). }[/math]
  1. Set [math]\displaystyle{ V_T = \{V_G\}, \ E_T = \empty. }[/math]
  2. Choose some [math]\displaystyle{ X \in V_T }[/math] with |X| ≥ 2 if such X exists. Otherwise, go to step 6.
  3. For each connected component [math]\displaystyle{ C = (V_C,E_C) \in T \setminus X, }[/math] let [math]\displaystyle{ S_C = \bigcup_{v_T \in V_C} v_T. }[/math]
    Let [math]\displaystyle{ S = \{ S_C \mid C \text{ is a connected component in } T \setminus X \}. }[/math]
    Contract the components to form [math]\displaystyle{ G' = ((V_{G'}, E_{G'}), c'), }[/math] where:[math]\displaystyle{ \begin{align} V_{G'} &= X \cup S \\[2pt] E_{G'} &= E_G|_{X \times X} \cup \{(u, S_C) \in X \times S \mid (u,v) \in E_G \text{ for some } v \in S_C \} \\[2pt] & \qquad \qquad \quad\! \cup \{(S_{C1}, S_{C2}) \in S \times S \mid (u,v) \in E_G \text{ for some } u \in S_{C1} \text{ and } v \in S_{C2} \} \end{align} }[/math]
    [math]\displaystyle{ c':V_{G'} \times V_{G'} \to R^+ }[/math] is the capacity function, defined as:[math]\displaystyle{ \begin{align} &\text{if }\ (u,S_C) \in E_G|_{X \times S}: &&c'(u,S_C) = \!\!\! \sum_{\begin{smallmatrix} v \in S_C : \\ (u,v) \in E_G \end{smallmatrix}} \!\!\! c(u,v) \\[4pt] &\text{if }\ (S_{C1},S_{C2}) \in E_G|_{S \times S}: &&c'(S_{C1},S_{C2}) = \!\!\!\!\!\!\! \sum_{\begin{smallmatrix} (u,v) \in E_G : \\ u \in S_{C1} \, \land \, v \in S_{C2} \end{smallmatrix}} \!\!\!\!\! c(u,v) \\[4pt] &\text{otherwise}: &&c'(u,v) = c(u,v) \end{align} }[/math]
  4. Choose two vertices s, t ∈ X and find a minimum s-t cut (A′, B′) in G'.
    Set [math]\displaystyle{ A = \Biggl(\bigcup_{S_C \in A' \cap S} \!\!\! S_C \! \Biggr) \cup (A' \cap X),\ }[/math][math]\displaystyle{ B = \Biggl(\bigcup_{S_C \in B' \cap S} \!\!\! S_C \! \Biggr) \cup (B' \cap X). }[/math]
  5. Set [math]\displaystyle{ V_T = (V_T \setminus X) \cup \{A \cap X, B \cap X \}. }[/math]
    For each [math]\displaystyle{ e = (X, Y) \in E_T }[/math] do:
    1. Set [math]\displaystyle{ e' = (A \cap X,Y) }[/math] if [math]\displaystyle{ Y \subset A, }[/math] otherwise set [math]\displaystyle{ e' = (B \cap X,Y). }[/math]
    2. Set [math]\displaystyle{ E_T = (E_T \setminus \{e\}) \cup \{e'\}. }[/math]
    3. Set [math]\displaystyle{ w(e') = w(e). }[/math]
    Set [math]\displaystyle{ E_T = E_T \cup \{(A \cap X,\ B \cap X) \}. }[/math]
    Set [math]\displaystyle{ w((A \cap X, B \cap X)) = c'(A', B'). }[/math]
    Go to step 2.
  6. Replace each [math]\displaystyle{ \{v\} \in V_T }[/math] by v and each [math]\displaystyle{ (\{u\},\{v\}) \in E_T }[/math] by (u, v). Output T.

Analysis

Using the submodular property of the capacity function c, one has [math]\displaystyle{ c(X) + c(Y) \ge c(X \cap Y) + c(X \cup Y). }[/math] Then it can be shown that the minimum s-t cut in G' is also a minimum s-t cut in G for any s, t ∈ X.

To show that for all [math]\displaystyle{ (P,Q) \in E_T, }[/math] [math]\displaystyle{ w(P,Q) = \lambda_{pq} }[/math] for some p ∈ P, q ∈ Q throughout the algorithm, one makes use of the following Lemma,

For any i, j, k in VG, [math]\displaystyle{ \lambda_{ik} \ge \min(\lambda_{ij}, \lambda_{jk}). }[/math]

The Lemma can be used again repeatedly to show that the output T satisfies the properties of a Gomory–Hu Tree.

Example

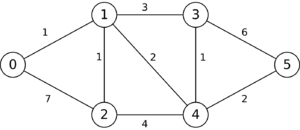
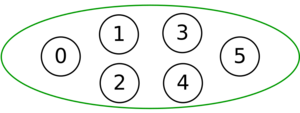
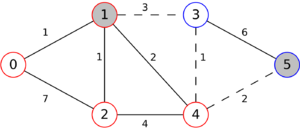
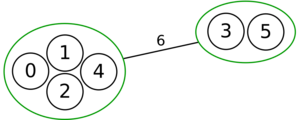
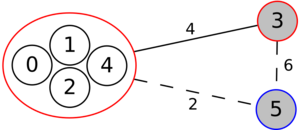
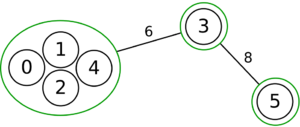
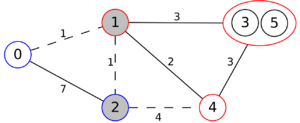
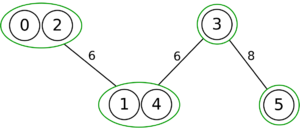
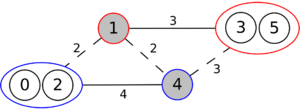
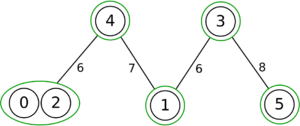
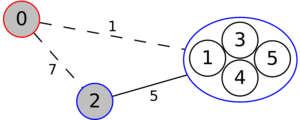
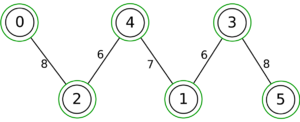
The following is a simulation of the Gomory–Hu's algorithm, where

  1. green circles are vertices of T.
  2. red and blue circles are the vertices in G'.
  3. grey vertices are the chosen s and t.
  4. red and blue coloring represents the s-t cut.
  5. dashed edges are the s-t cut-set.
  6. A is the set of vertices circled in red and B is the set of vertices circled in blue.
G' T
Gomory–Hu G.svg Gomory–Hu T.svg
1. Set VT = {VG} = { {0, 1, 2, 3, 4, 5} } and ET = ∅.
2. Since VT has only one vertex, choose X = VG = {0, 1, 2, 3, 4, 5}. Note that | X | = 6 ≥ 2.
1. Gomory–Hu Gp1.svg Gomory–Hu T1.svg
3. Since T\X = ∅, there is no contraction and therefore G' = G.
4. Choose s = 1 and t = 5. The minimum s-t cut (A', B') is ({0, 1, 2, 4}, {3, 5}) with c'(A', B') = 6.
    Set A = {0, 1, 2, 4} and B = {3, 5}.
5. Set VT = (VT\X) ∪ {A ∩ X, B ∩ X} = { {0, 1, 2, 4}, {3, 5} }.
    Set ET = { ({0, 1, 2, 4}, {3, 5}) }.
    Set w( ({0, 1, 2, 4}, {3, 5}) ) = c'(A', B') = 6.
    Go to step 2.
2. Choose X = {3, 5}. Note that | X | = 2 ≥ 2.
2. Gomory–Hu Gp2.svg Gomory–Hu T2.svg
3. {0, 1, 2, 4} is the connected component in T\X and thus S = { {0, 1, 2, 4} }.
    Contract {0, 1, 2, 4} to form G', where
c'( (3, {0, 1, 2 ,4}) ) = c( (3, 1) ) + c( (3, 4) ) = 4.
c'( (5, {0, 1, 2, 4}) ) = c( (5, 4) ) = 2.
c'( (3, 5)) = c( (3, 5) ) = 6.
4. Choose s = 3, t = 5. The minimum s-t cut (A', B') in G' is ( {{0, 1, 2, 4}, 3}, {5} ) with c'(A', B') = 8.
    Set A = {0, 1, 2, 3, 4} and B = {5}.
5. Set VT = (VT\X) ∪ {A ∩ X, B ∩ X} = { {0, 1, 2, 4}, {3}, {5} }.
    Since (X, {0, 1, 2, 4}) ∈ ET and {0, 1, 2, 4} ⊂ A, replace it with (A ∩ X, Y) = ({3}, {0, 1, 2 ,4}).
    Set ET = { ({3}, {0, 1, 2 ,4}), ({3}, {5}) } with
w(({3}, {0, 1, 2 ,4})) = w((X, {0, 1, 2, 4})) = 6.
w(({3}, {5})) = c'(A', B') = 8.
    Go to step 2.
2. Choose X = {0, 1, 2, 4}. Note that | X | = 4 ≥ 2.
3. Gomory–Hu Gp3.svg Gomory–Hu T3.svg
3. { {3}, {5} } is the connected component in T\X and thus S = { {3, 5} }.
    Contract {3, 5} to form G', where
c'( (1, {3, 5}) ) = c( (1, 3) ) = 3.
c'( (4, {3, 5}) ) = c( (4, 3) ) + c( (4, 5) ) = 3.
c'(u,v) = c(u,v) for all u,v ∈ X.
4. Choose s = 1, t = 2. The minimum s-t cut (A', B') in G' is ( {1, {3, 5}, 4}, {0, 2} ) with c'(A', B') = 6.
    Set A = {1, 3, 4, 5} and B = {0, 2}.
5. Set VT = (VT\X) ∪ {A ∩ X, B ∩ X} = { {3}, {5}, {1, 4}, {0, 2} }.
    Since (X, {3}) ∈ ET and {3} ⊂ A, replace it with (A ∩ X, Y) = ({1, 4}, {3}).
    Set ET = { ({1, 4}, {3}), ({3}, {5}), ({0, 2}, {1, 4}) } with
w(({1, 4}, {3})) = w((X, {3})) = 6.
w(({0, 2}, {1, 4})) = c'(A', B') = 6.
    Go to step 2.
2. Choose X = {1, 4}. Note that | X | = 2 ≥ 2.
4. Gomory–Hu Gp4.svg Gomory–Hu T4.svg
3. { {3}, {5} }, { {0, 2} } are the connected components in T\X and thus S = { {0, 2}, {3, 5} }
    Contract {0, 2} and {3, 5} to form G', where
c'( (1, {3, 5}) ) = c( (1, 3) ) = 3.
c'( (4, {3, 5}) ) = c( (4, 3) ) + c( (4, 5) ) = 3.
c'( (1, {0, 2}) ) = c( (1, 0) ) + c( (1, 2) ) = 2.
c'( (4, {0, 2}) ) = c( (4, 2) ) = 4.
c'(u,v) = c(u,v) for all u,v ∈ X.
4. Choose s = 1, t = 4. The minimum s-t cut (A', B') in G' is ( {1, {3, 5}}, {{0, 2}, 4} ) with c'(A', B') = 7.
    Set A = {1, 3, 5} and B = {0, 2, 4}.
5. Set VT = (VT\X) ∪ {A ∩ X, B ∩ X} = { {3}, {5}, {0, 2}, {1}, {4} }.
    Since (X, {3}) ∈ ET and {3} ⊂ A, replace it with (A ∩ X, Y) = ({1}, {3}).
    Since (X, {0, 2}) ∈ ET and {0, 2} ⊂ B, replace it with (B ∩ X, Y) = ({4}, {0, 2}).
    Set ET = { ({1}, {3}), ({3}, {5}), ({4}, {0, 2}), ({1}, {4}) } with
w(({1}, {3})) = w((X, {3})) = 6.
w(({4}, {0, 2})) = w((X, {0, 2})) = 6.
w(({1}, {4})) = c'(A', B') = 7.
    Go to step 2.
2. Choose X = {0, 2}. Note that | X | = 2 ≥ 2.
5. Gomory–Hu Gp5.svg Gomory–Hu T5.svg
3. { {1}, {3}, {4}, {5} } is the connected component in T\X and thus S = { {1, 3, 4, 5} }.
    Contract {1, 3, 4, 5} to form G', where
c'( (0, {1, 3, 4, 5}) ) = c( (0, 1) ) = 1.
c'( (2, {1, 3, 4, 5}) ) = c( (2, 1) ) + c( (2, 4) ) = 5.
c'( (0, 2) ) = c( (0, 2) ) = 7.
4. Choose s = 0, t = 2. The minimum s-t cut (A', B') in G' is ( {0}, {2, {1, 3, 4, 5}} ) with c'(A', B') = 8.
    Set A = {0} and B = {1, 2, 3 ,4 ,5}.
5. Set VT = (VT\X) ∪ {A ∩ X, B ∩ X} = { {3}, {5}, {1}, {4}, {0}, {2} }.
    Since (X, {4}) ∈ ET and {4} ⊂ B, replace it with (B ∩ X, Y) = ({2}, {4}).
    Set ET = { ({1}, {3}), ({3}, {5}), ({2}, {4}), ({1}, {4}), ({0}, {2}) } with
w(({2}, {4})) = w((X, {4})) = 6.
w(({0}, {2})) = c'(A', B') = 8.
    Go to step 2.
2. There does not exist X∈VT with | X | ≥ 2. Hence, go to step 6.
6.

Gomory–Hu output.svg

6. Replace VT = { {3}, {5}, {1}, {4}, {0}, {2} } by {3, 5, 1, 4, 0, 2}.
    Replace ET = { ({1}, {3}), ({3}, {5}), ({2}, {4}), ({1}, {4}), ({0}, {2}) } by { (1, 3), (3, 5), (2, 4), (1, 4), (0, 2) }.
    Output T. Note that exactly | V | − 1 = 6 − 1 = 5 times min-cut computation is performed.

Implementations: Sequential and Parallel

Gusfield's algorithm can be used to find a Gomory–Hu tree without any vertex contraction in the same running time-complexity, which simplifies the implementation of constructing a Gomory–Hu Tree.[2]

Andrew V. Goldberg and K. Tsioutsiouliklis implemented the Gomory-Hu algorithm and Gusfield algorithm, and performed an experimental evaluation and comparison.[3]

Cohen et al. report results on two parallel implementations of Gusfield's algorithm using OpenMP and MPI, respectively.[4]

Related concepts

In planar graphs, the Gomory–Hu tree is dual to the minimum weight cycle basis, in the sense that the cuts of the Gomory–Hu tree are dual to a collection of cycles in the dual graph that form a minimum-weight cycle basis.[5]

See also

References

  1. ↑ Gomory, R. E.; Hu, T. C. (1961). "Multi-terminal network flows". Journal of the Society for Industrial and Applied Mathematics 9 (4): 551–570. doi:10.1137/0109047. 
  2. ↑ Gusfield, Dan (1990). "Very Simple Methods for All Pairs Network Flow Analysis". SIAM J. Comput. 19 (1): 143–155. doi:10.1137/0219009. 
  3. ↑ Goldberg, A. V.; Tsioutsiouliklis, K. (2001). "Cut Tree Algorithms: An Experimental Study". Journal of Algorithms 38 (1): 51–83. doi:10.1006/jagm.2000.1136. 
  4. ↑ Cohen, Jaime; Rodrigues, Luiz A.; Silva, Fabiano; Carmo, Renato; Guedes, André Luiz Pires; Duarte, Jr., Elias P. (2011). "Algorithms and Architectures for Parallel Processing – 11th International Conference, ICA3PP, Melbourne, Australia, October 24–26, 2011, Proceedings, Part I". in Xiang, Yang; Cuzzocrea, Alfredo; Hobbs, Michael et al.. 7016. Springer. pp. 258–269. doi:10.1007/978-3-642-24650-0_22. 
  5. ↑ Hartvigsen, D.; Mardon, R. (1994). "The all-pairs min cut problem and the minimum cycle basis problem on planar graphs". SIAM J. Discrete Math. 7 (3): 403–418. doi:10.1137/S0895480190177042. .



Retrieved from "https://handwiki.org/wiki/index.php?title=Gomory–Hu_tree&oldid=3360985"