Good regulator

Short description: Theorem in cybernetics

The good regulator is a theorem conceived by Roger C. Conant and W. Ross Ashby that is central to cybernetics. Originally stated that "every good regulator of a system must be a model of that system", but more accurately, every good regulator must contain a model of the system. That is, any regulator that is maximally simple among optimal regulators must behave as an image of that system under a homomorphism; while the authors sometimes say 'isomorphism', the mapping they construct is only a homomorphism.

Theorem

This theorem is obtained by considering the entropy of the variation of the output of the controlled system, and shows that, under very general conditions, that the entropy is minimized when there is a (deterministic) mapping [math]\displaystyle{ h:S\to R }[/math] from the states of the system to the states of the regulator. The authors view this map [math]\displaystyle{ h }[/math] as making the regulator a 'model' of the system.

With regard to the brain, insofar as it is successful and efficient as a regulator for survival, it must proceed, in learning, by the formation of a model (or models) of its environment.

The theorem is general enough to apply to all regulating and self-regulating or homeostatic systems.

Variables involved in good regulation as according to the authors.

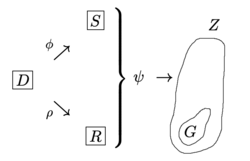
Five variables are defined by the authors as involved in the process of system regulation. [math]\displaystyle{ D }[/math] as primary disturbers, [math]\displaystyle{ R }[/math] as a set of events in the regulator, [math]\displaystyle{ S }[/math] as a set of events in the rest of the system outside of the regulator, [math]\displaystyle{ Z }[/math] as the total set of events (or outcomes) that may occur, [math]\displaystyle{ G }[/math] as the subset of [math]\displaystyle{ Z }[/math] events (or outcomes) that are desirable to the system.

The principal point that the authors present with this figure is that regulation requires of the regulator to conceive of all variables as it regards the set [math]\displaystyle{ S }[/math] of events concerning the system to be regulated in order to render in satisfactory outcomes [math]\displaystyle{ G }[/math] of this regulation. If the regulator is instead not able to conceive of all variables in the set [math]\displaystyle{ S }[/math] of events concerning the system that exist outside of the regulator, then the set [math]\displaystyle{ R }[/math] of events in the regulator may fail to account for the total variable disturbances [math]\displaystyle{ D }[/math] which in turn may cause errors that lead to outcomes that are not satisfactory to the system (as illustrated by the events in the set [math]\displaystyle{ Z }[/math] that are not elements in the set [math]\displaystyle{ G }[/math]).

The theorem does not explain what it takes for the system to become a good regulator. In cybernetics, the problem of creating good regulators is addressed by the ethical regulator theorem, and by the theory of practopoiesis. The construction of good regulators is a general problem for any system (e.g., an automated information system) that regulates some domain of application.

When restricted to the ordinary differential equation (ODE) subset of control theory, it is referred to as the internal model principle, which was first articulated in 1976 by B. A. Francis and W. M. Wonham. In this form, it stands in contrast to classical control, in that the classical feedback loop fails to explicitly model the controlled system (although the classical controller may contain an implicit model).

See also

• Analogy
• Internal model (motor control)
• Map–territory relation
• Variety (cybernetics)