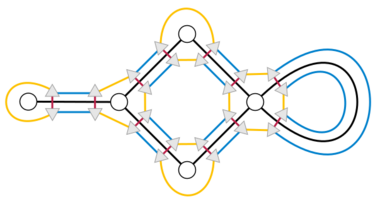
Graph-encoded map

Short description: Graph describing a topological embedding

A graph-encoded map (gray triangles and colored edges) of a graph in the plane (white circles and black edges)

In topological graph theory, a graph-encoded map or gem is a method of encoding a cellular embedding of a graph using a different graph with four vertices per edge of the original graph. It is the topological analogue of runcination, a geometric operation on polyhedra. Graph-encoded maps were formulated and named by (Lins 1982). Alternative and equivalent systems for representing cellular embeddings include signed rotation systems and ribbon graphs.

The graph-encoded map for an embedded graph [math]\displaystyle{ G }[/math] is another cubic graph [math]\displaystyle{ H }[/math] together with a 3-edge-coloring of [math]\displaystyle{ H }[/math]. Each edge [math]\displaystyle{ e }[/math] of [math]\displaystyle{ G }[/math] is expanded into exactly four vertices in [math]\displaystyle{ H }[/math], one for each choice of a side and endpoint of the edge. An edge in [math]\displaystyle{ H }[/math] connects each such vertex to the vertex representing the opposite side and same endpoint of [math]\displaystyle{ e }[/math]; these edges are by convention colored red. Another edge in [math]\displaystyle{ H }[/math] connects each vertex to the vertex representing the opposite endpoint and same side of [math]\displaystyle{ e }[/math]; these edges are by convention colored blue. An edge in [math]\displaystyle{ H }[/math] of the third color, yellow, connects each vertex to the vertex representing another edge [math]\displaystyle{ e' }[/math] that meets [math]\displaystyle{ e }[/math] at the same side and endpoint.

An alternative description of [math]\displaystyle{ H }[/math] is that it has a vertex for each flag of [math]\displaystyle{ G }[/math] (a mutually incident triple of a vertex, edge, and face). If [math]\displaystyle{ (v,e,f) }[/math] is a flag, then there is exactly one vertex [math]\displaystyle{ v' }[/math], edge [math]\displaystyle{ e' }[/math], and face [math]\displaystyle{ f' }[/math] such that [math]\displaystyle{ (v',e,f) }[/math], [math]\displaystyle{ (v,e',f) }[/math], and [math]\displaystyle{ (v,e,f') }[/math] are also flags. The three colors of edges in [math]\displaystyle{ H }[/math] represent each of these three types of flags that differ by one of their three elements. However, interpreting a graph-encoded map in this way requires more care. When the same face appears on both sides of an edge, as can happen for instance for a planar embedding of a tree, the two sides give rise to different gem vertices. And when the same vertex appears at both endpoints of a self-loop, the two ends of the edge again give rise to different gem vertices. In this way, each triple [math]\displaystyle{ (v,e,f) }[/math] may be associated with up to four different vertices of the gem.

Whenever a cubic graph [math]\displaystyle{ H }[/math] can be 3-edge-colored so that the red-blue cycles of the coloring all have length four, the colored graph can be interpreted as a graph-encoded map, and represents an embedding of another graph [math]\displaystyle{ G }[/math]. To recover [math]\displaystyle{ G }[/math] and its embedding, interpret each 2-colored cycle of [math]\displaystyle{ H }[/math] as the face of an embedding of [math]\displaystyle{ H }[/math] onto a surface, contract each red--yellow cycle into a single vertex of [math]\displaystyle{ G }[/math], and replace each pair of parallel blue edges left by the contraction with a single edge of [math]\displaystyle{ G }[/math].

The dual graph of a graph-encoded map may be obtained from the map by recoloring it so that the red edges of the gem become blue and the blue edges become red.