Graph product

In mathematics, a graph product is a binary operation on graphs. Specifically, it is an operation that takes two graphs G₁ and G₂ and produces a graph H with the following properties:

• The vertex set of H is the Cartesian product V(G₁) × V(G₂), where V(G₁) and V(G₂) are the vertex sets of G₁ and G₂, respectively.
• Two vertices (u₁, u₂) and (v₁, v₂) of H are connected by an edge if and only if the vertices u₁, u₂, v₁, v₂ satisfy a condition that takes into account the edges of G₁ and G₂. The graph products differ in exactly which this condition is.

The terminology and notation for specific graph products in the literature varies quite a lot; even if the following may be considered somewhat standard, readers are advised to check what definition a particular author uses for a graph product, especially in older texts.

Overview table

The following table shows the most common graph products, with [math]\displaystyle{ \sim }[/math] denoting “is connected by an edge to”, and [math]\displaystyle{ \not\sim }[/math] denoting non-connection. The operator symbols listed here are by no means standard, especially in older papers.

Name	Condition for [math]\displaystyle{ (u_1,u_2)\sim(v_1,v_2) }[/math]	Number of edges [math]\displaystyle{ \begin{array}{cc} n_1 = \vert\mathrm{V}(G_1)\vert & n_2 = \vert\mathrm{V}(G_2)\vert \\ m_1 = \vert\mathrm{E}(G_1)\vert & m_2 = \vert\mathrm{E}(G_2)\vert \end{array} }[/math]	Example
Cartesian product [math]\displaystyle{ G 1 \square G 2 }[/math]	( [math]\displaystyle{ u_1 }[/math] = [math]\displaystyle{ v_1 }[/math] and [math]\displaystyle{ u_2 }[/math] [math]\displaystyle{ \sim }[/math] [math]\displaystyle{ v_2 }[/math] ) or ( [math]\displaystyle{ u_1 }[/math] [math]\displaystyle{ \sim }[/math] [math]\displaystyle{ v_1 }[/math] and [math]\displaystyle{ u_2 }[/math] = [math]\displaystyle{ v_2 }[/math] )	[math]\displaystyle{ m_2 n_1 + m_1 n_2 }[/math]
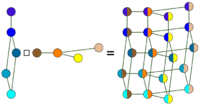
Tensor product (Kronecker product, categorical product) [math]\displaystyle{ G_1 \times G_2 }[/math]	[math]\displaystyle{ u_1 }[/math] [math]\displaystyle{ \sim }[/math] [math]\displaystyle{ v_1 }[/math] and  [math]\displaystyle{ u_2 }[/math] [math]\displaystyle{ \sim }[/math] [math]\displaystyle{ v_2 }[/math]	[math]\displaystyle{ 2 m_1 m_2 }[/math]
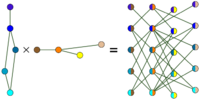
Lexicographical product [math]\displaystyle{ G_1 \cdot G_2 }[/math] or [math]\displaystyle{ G_1[G_2] }[/math]	u1 ∼ v1 or ( u1 = v1 and u2 ∼ v2 )	[math]\displaystyle{ m_2 n_1 + m_1 n_2^2 }[/math]
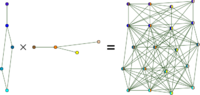
Strong product (Normal product, AND product) [math]\displaystyle{ G_1 \boxtimes G_2 }[/math]	( u1 = v1 and u2 ∼ v2 ) or ( u1 ∼ v1 and u2 = v2 ) or ( u1 ∼ v1 and u2 ∼ v2 )	[math]\displaystyle{ n_1 m_2 + n_2 m_1 + 2 m_1 m_2 }[/math]
Co-normal product (disjunctive product, OR product) [math]\displaystyle{ G_1 * G_2 }[/math]	u1 ∼ v1 or u2 ∼ v2
Modular product	[math]\displaystyle{ (u_1 \sim v_1 \text{ and } u_2 \sim v_2) }[/math] or [math]\displaystyle{ (u_1 \not\sim v_1 \text{ and } u_2 \not\sim v_2) }[/math]
Rooted product	see article	[math]\displaystyle{ m_2 n_1 + m_1 }[/math]	File:Graph-rooted-product.svg
Zig-zag product	see article	see article	see article
Replacement product
Homomorphic product [math]\displaystyle{ G_1 \ltimes G_2 }[/math]	[math]\displaystyle{ (u_1 = v_1) }[/math] or [math]\displaystyle{ (u_1 \sim v_1 \text{ and } u_2 \not\sim v_2) }[/math]

In general, a graph product is determined by any condition for (u₁, u₂) ∼ (v₁, v₂) that can be expressed in terms of the statements u₁ ∼ v₁, u₂ ∼ v₂, u₁ = v₁, and u₂ = v₂.

Mnemonic

Let [math]\displaystyle{ K_2 }[/math] be the complete graph on two vertices (i.e. a single edge). The product graphs [math]\displaystyle{ K_2 \square K_2 }[/math], [math]\displaystyle{ K_2 \times K_2 }[/math], and [math]\displaystyle{ K_2 \boxtimes K_2 }[/math] look exactly like the graph representing the operator. For example, [math]\displaystyle{ K_2 \square K_2 }[/math] is a four cycle (a square) and [math]\displaystyle{ K_2 \boxtimes K_2 }[/math] is the complete graph on four vertices. The [math]\displaystyle{ G_1[G_2] }[/math] notation for lexicographic product serves as a reminder that this product is not commutative.

See also

• Graph operations

References

• Imrich, Wilfried; Klavžar, Sandi (2000). Product Graphs: Structure and Recognition. Wiley. ISBN 978-0-471-37039-0{{inconsistent citations}} .