Great stellated truncated dodecahedron
| Great stellated truncated dodecahedron | |
|---|---|

| |
| Type | Uniform star polyhedron |
| Elements | F = 32, E = 90 V = 60 (χ = 2) |
| Faces by sides | 20{3}+12{10/3} |
| Wythoff symbol | 2 3 | 5/3 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U66, C83, W104 |
| Dual polyhedron | Great triakis icosahedron |
| Vertex figure |  3.10/3.10/3 |
| Bowers acronym | Quit Gissid |
File:Great stellated truncated dodecahedron.stl
In geometry, the great stellated truncated dodecahedron (or quasitruncated great stellated dodecahedron or great stellatruncated dodecahedron) is a nonconvex uniform polyhedron, indexed as U66. It has 32 faces (20 triangles and 12 decagrams), 90 edges, and 60 vertices.[1] It is given a Schläfli symbol t0,1{5/3,3}.
Related polyhedra
It shares its vertex arrangement with three other uniform polyhedra: the small icosicosidodecahedron, the small ditrigonal dodecicosidodecahedron, and the small dodecicosahedron:
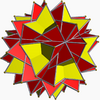 Great stellated truncated dodecahedron |
 Small icosicosidodecahedron |
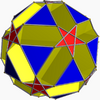 Small ditrigonal dodecicosidodecahedron |
 Small dodecicosahedron |
Cartesian coordinates
Cartesian coordinates for the vertices of a great stellated truncated dodecahedron are all the even permutations of [math]\displaystyle{ \begin{array}{crclc} \Bigl(& 0,& \pm\,\varphi,& \pm \bigl[2-\frac{1}{\varphi}\bigr] &\Bigr) \\ \Bigl(& \pm\,\varphi,& \pm\,\frac{1}{\varphi},& \pm\,\frac{2}{\varphi} &\Bigr) \\ \Bigl(& \pm\,\frac{1}{\varphi^2},& \pm\,\frac{1}{\varphi},& \pm\,2 &\Bigr) \end{array} }[/math]
where [math]\displaystyle{ \varphi = \tfrac{1+\sqrt 5}{2} }[/math] is the golden ratio.
See also
References
External links
- Weisstein, Eric W.. "Great stellated truncated dodecahedron". http://mathworld.wolfram.com/GreatStellatedTruncatedDodecahedron.html.
 |

