Uniform star polyhedron


In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both.
The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedra, 5 quasiregular ones, and 48 semiregular ones.
There are also two infinite sets of uniform star prisms and uniform star antiprisms.
Just as (nondegenerate) star polygons (which have polygon density greater than 1) correspond to circular polygons with overlapping tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhedra with overlapping tiles; there are 47 nonprismatic such uniform star polyhedra. The remaining 10 nonprismatic uniform star polyhedra, those that pass through the center, are the hemipolyhedra as well as Miller's monster, and do not have well-defined densities.
The nonconvex forms are constructed from Schwarz triangles.
All the uniform polyhedra are listed below by their symmetry groups and subgrouped by their vertex arrangements.
Regular polyhedra are labeled by their Schläfli symbol. Other nonregular uniform polyhedra are listed with their vertex configuration.
An additional figure, the pseudo great rhombicuboctahedron, is usually not included as a truly uniform star polytope, despite consisting of regular faces and having the same vertices.
Note: For nonconvex forms below an additional descriptor nonuniform is used when the convex hull vertex arrangement has same topology as one of these, but has nonregular faces. For example an nonuniform cantellated form may have rectangles created in place of the edges rather than squares.
Dihedral symmetry
See Prismatic uniform polyhedron.
Tetrahedral symmetry

There is one nonconvex form, the tetrahemihexahedron which has tetrahedral symmetry (with fundamental domain Möbius triangle (3 3 2)).
There are two Schwarz triangles that generate unique nonconvex uniform polyhedra: one right triangle (3⁄2 3 2), and one general triangle (3⁄2 3 3). The general triangle (3⁄2 3 3) generates the octahemioctahedron which is given further on with its full octahedral symmetry.
| Vertex arrangement (Convex hull) |
Nonconvex forms | |
|---|---|---|
 Tetrahedron |
||
 Rectified tetrahedron Octahedron |
 4.3⁄2.4.3 3⁄2 3 | 2 | |
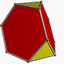 Truncated tetrahedron |
||
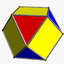 Cantellated tetrahedron (Cuboctahedron) |
||
 Omnitruncated tetrahedron (Truncated octahedron) |
||
 Snub tetrahedron (Icosahedron) |
||
Octahedral symmetry

There are 8 convex forms, and 10 nonconvex forms with octahedral symmetry (with fundamental domain Möbius triangle (4 3 2)).
There are four Schwarz triangles that generate nonconvex forms, two right triangles (3⁄2 4 2), and (4⁄3 3 2), and two general triangles: (4⁄3 4 3), (3⁄2 4 4).
| Vertex arrangement (Convex hull) |
Nonconvex forms | ||
|---|---|---|---|
 Cube |
|||
 Octahedron |
|||
 Cuboctahedron |
 6.4⁄3.6.4 4⁄3 4 | 3 |
 6.3⁄2.6.3 3⁄2 3 | 3 | |
 Truncated cube |
 4.8⁄3.4⁄3.8⁄5 2 4⁄3 (3⁄2 4⁄2) | |
 8⁄3.3.8⁄3.4 3 4 | 4⁄3 |
 4.3⁄2.4.4 3⁄2 4 | 2 |
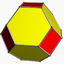 Truncated octahedron |
|||
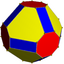
 Rhombicuboctahedron |
 4.8.4⁄3.8 2 4 (3⁄2 4⁄2) | |
 8.3⁄2.8.4 3⁄2 4 | 4 |
 8⁄3.8⁄3.3 2 3 | 4⁄3 |
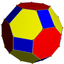 Nonuniform truncated cuboctahedron |
 4.6.8⁄3 2 3 4⁄3 | | ||
 Nonuniform truncated cuboctahedron |
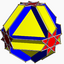 8⁄3.6.8 3 4 4⁄3 | | ||
 Snub cube |
|||
Icosahedral symmetry

There are 8 convex forms and 46 nonconvex forms with icosahedral symmetry (with fundamental domain Möbius triangle (5 3 2)). (or 47 nonconvex forms if Skilling's figure is included). Some of the nonconvex snub forms have reflective vertex symmetry.
Degenerate cases
Coxeter identified a number of degenerate star polyhedra by the Wythoff construction method, which contain overlapping edges or vertices. These degenerate forms include:
- Small complex icosidodecahedron
- Great complex icosidodecahedron
- Small complex rhombicosidodecahedron
- Great complex rhombicosidodecahedron
- Complex rhombidodecadodecahedron
Skilling's figure
One further nonconvex degenerate polyhedron is the great disnub dirhombidodecahedron, also known as Skilling's figure, which is vertex-uniform, but has pairs of edges which coincide in space such that four faces meet at some edges. It is counted as a degenerate uniform polyhedron rather than a uniform polyhedron because of its double edges. It has Ih symmetry.
See also
References
- Coxeter, H. S. M. (May 13, 1954). "Uniform Polyhedra". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 246 (916): 401–450. doi:10.1098/rsta.1954.0003.
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. OCLC 1738087.
- Brückner, M. Vielecke und vielflache. Theorie und geschichte.. Leipzig, Germany: Teubner, 1900. [1]
- Sopov, S. P. (1970), "A proof of the completeness on the list of elementary homogeneous polyhedra", Ukrainskiui Geometricheskiui Sbornik (8): 139–156
- Skilling, J. (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 278: 111–135, doi:10.1098/rsta.1975.0022, ISSN 0080-4614
- Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El, Kaleido software, Images, dual images
- Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993. [2]
- Messer, Peter W. Closed-Form Expressions for Uniform Polyhedra and Their Duals., Discrete & Computational Geometry 27:353-375 (2002).
- Klitzing, Richard. "3D uniform polyhedra". https://bendwavy.org/klitzing/dimensions/polyhedra-neu.htm.
External links
 |