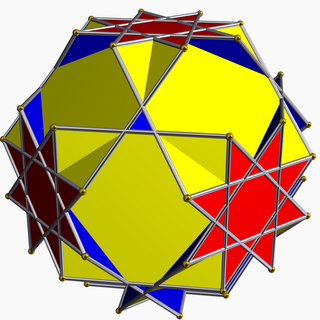
Great truncated cuboctahedron
| Great truncated cuboctahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 26, E = 72 V = 48 (χ = 2) |
| Faces by sides | 12{4}+8{6}+6{8/3} |
| Wythoff symbol | 2 3 4/3 | |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U20, C67, W93 |
| Dual polyhedron | Great disdyakis dodecahedron |
| Vertex figure | 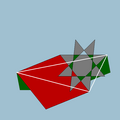 4.6/5.8/3 |
| Bowers acronym | Quitco |
File:Great truncated cuboctahedron.stl
In geometry, the great truncated cuboctahedron (or quasitruncated cuboctahedron or stellatruncated cuboctahedron) is a nonconvex uniform polyhedron, indexed as U20. It has 26 faces (12 squares, 8 hexagons and 6 octagrams), 72 edges, and 48 vertices.[1] It is represented by the Schläfli symbol tr{4/3,3}, and Coxeter-Dynkin diagram 
. It is sometimes called the quasitruncated cuboctahedron because it is related to the truncated cuboctahedron, , except that the octagonal faces are replaced by {8/3} octagrams.
Convex hull
Its convex hull is a nonuniform truncated cuboctahedron. The truncated cuboctahedron and the great truncated cuboctahedron form isomorphic graphs despite their different geometric structure.
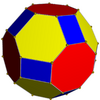 Convex hull |
Great truncated cuboctahedron |
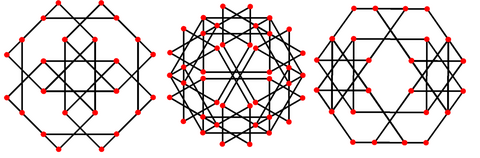
Orthographic projections
Cartesian coordinates
Cartesian coordinates for the vertices of a great truncated cuboctahedron centered at the origin are all permutations of [math]\displaystyle{ \Bigl( \pm 1, \ \pm\left[1-\sqrt 2 \right], \ \pm\left[1-2\sqrt 2\right]\Bigr). }[/math]
See also
References
External links
- Weisstein, Eric W.. "Great truncated cuboctahedron". http://mathworld.wolfram.com/GreatTruncatedCuboctahedron.html.
 |  |
