Guillotine problem
From HandWiki
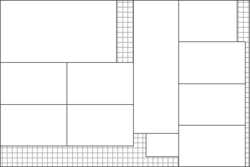
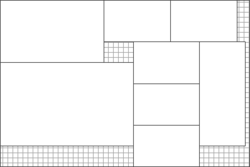
The guillotine problem is a problem in combinatorial geometry and in printing.
Closely related to packing problems and specifically to cutting stock and bin packing problems,[1] it is the question of how to get the maximum number of sheets of one rectangular size out of a larger sheet, only orthogonal cuts that bisect one component of the sheet are allowed, as on a paper cutting guillotine.
The Guillotine problem is important in glass machining. Glass sheets are scored along horizontal and vertical lines and then broken along these lines to obtain smaller panels.[2]
Like the cutting stock problem, it is NP hard, but various approximate and exact solutions have been devised.[3][4][5]
References
- ↑ Gerhard Wäscher, Heike Haußner, Holger Schumann, An improved typology of cutting and packing problems, European Journal of Operational Research 183 (2007) 1109–1130, [1]
- ↑ Tlilane, Lydia; Viaud, Quentin (2018-05-18). "Challenge ROADEF / EURO 2018 Cutting Optimization Problem Description". ROADEF. http://www.roadef.org/challenge/2018/files/Challenge_ROADEF_EURO_SG_Description.pdf#page=2.
- ↑ Michael L. McHale, Roshan P. Shah Cutting the Guillotine Down to Size. PC AI magazine, Volume 13, Number 1 Jan/Feb 99. http://www.amzi.com/articles/papercutter.htm
- ↑ M. Hifi, R. M’Hallah and T. Saadi, Approximate and exact algorithms for the double-constrained two-dimensional guillotine cutting stock problem. Computational Optimization and Applications, Volume 42, Number 2 (2009), 303-326, doi:10.1007/s10589-007-9081-5
- ↑ François Clautiaux, Antoine Jouglet, Aziz Moukrim, A New Graph-Theoretical Model for the Guillotine-Cutting Problem. INFORMS Journal on Computing October 2011 ijoc.1110.0478 pp. 1–15
