Hadamard test (quantum computation)

Short description: Technique in quantum computation

In quantum computation, the Hadamard test is a method used to create a random variable whose expected value is the expected real part [math]\displaystyle{ \mathrm{Re}\langle\psi| U|\psi\rangle }[/math], where [math]\displaystyle{ |\psi\rangle }[/math] is a quantum state and [math]\displaystyle{ U }[/math] is a unitary gate acting on the space of [math]\displaystyle{ |\psi\rangle }[/math]. The Hadamard test produces a random variable whose image is in [math]\displaystyle{ \{\pm 1\} }[/math] and whose expected value is exactly [math]\displaystyle{ \mathrm{Re}\langle\psi| U|\psi\rangle }[/math]. It is possible to modify the circuit to produce a random variable whose expected value is [math]\displaystyle{ \mathrm{Im}\langle\psi| U|\psi\rangle }[/math].

Description of the circuit

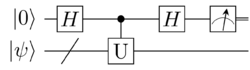
To perform the Hadamard test we first calculate the state [math]\displaystyle{ \frac{1}{\sqrt{2}}\left(\left|0\right\rangle +\left|1\right\rangle \right)\otimes\left|\psi\right\rangle }[/math]. We then apply the unitary operator on [math]\displaystyle{ \left|\psi\right\rangle }[/math] conditioned on the first qubit to obtain the state [math]\displaystyle{ \frac{1}{\sqrt{2}}\left(\left|0\right\rangle \otimes\left|\psi\right\rangle +\left|1\right\rangle \otimes U\left|\psi\right\rangle \right) }[/math]. We then apply the Hadamard gate to the first qubit, yielding [math]\displaystyle{ \frac{1}{2}\left(\left|0\right\rangle \otimes(I+U)\left|\psi\right\rangle +\left|1\right\rangle \otimes (I-U)\left|\psi\right\rangle \right) }[/math].

Measuring the first qubit, the result is [math]\displaystyle{ \left|0\right\rangle }[/math] with probability [math]\displaystyle{ \frac{1}{4}\langle\psi| (I+U^\dagger)(I+U)|\psi \rangle }[/math], in which case we output [math]\displaystyle{ 1 }[/math]. The result is [math]\displaystyle{ \left|1\right\rangle }[/math] with probability [math]\displaystyle{ \frac{1}{4}\langle\psi | (I-U^\dagger)(I-U)| \psi \rangle }[/math], in which case we output [math]\displaystyle{ -1 }[/math]. The expected value of the output will then be the difference between the two probabilities, which is [math]\displaystyle{ \frac{1}{2} \langle\psi| (U^\dagger+U)| \psi \rangle = \mathrm{Re}\langle\psi | U| \psi \rangle }[/math]

To obtain a random variable whose expectation is [math]\displaystyle{ \mathrm{Im}\langle\psi | U | \psi \rangle }[/math] follow exactly the same procedure but start with [math]\displaystyle{ \frac{1}{\sqrt{2}}\left(\left|0\right\rangle -i\left|1\right\rangle \right)\otimes\left|\psi\right\rangle }[/math].

The Hadamard test has many applications in quantum algorithms such as the Aharonov-Jones-Landau algorithm. Via a very simple modification it can be used to compute inner product between two states [math]\displaystyle{ |\phi_1\rangle }[/math] and [math]\displaystyle{ |\phi_2\rangle }[/math]: instead of starting from a state [math]\displaystyle{ |\psi\rangle }[/math] it suffice to start from the ground state [math]\displaystyle{ |0\rangle }[/math], and perform two controlled operations on the ancilla qubit. Controlled on the ancilla register being [math]\displaystyle{ |0\rangle }[/math], we apply the unitary that produces [math]\displaystyle{ |\phi_1\rangle }[/math] in the second register, and controlled on the ancilla register being in the state [math]\displaystyle{ |1\rangle }[/math], we create [math]\displaystyle{ |\phi_2\rangle }[/math] in the second register. The expected value of the measurements of the ancilla qubits leads to an estimate of [math]\displaystyle{ \langle \phi_1|\phi_2\rangle }[/math]. The number of samples needed to estimate the expected value with absolute error [math]\displaystyle{ \epsilon }[/math] is [math]\displaystyle{ O\left(\frac{1}{\epsilon^2}\right) }[/math], because of a Chernoff bound. This value can be improved to [math]\displaystyle{ O\left(\frac{1}{\epsilon}\right) }[/math] using amplitude estimation techniques.