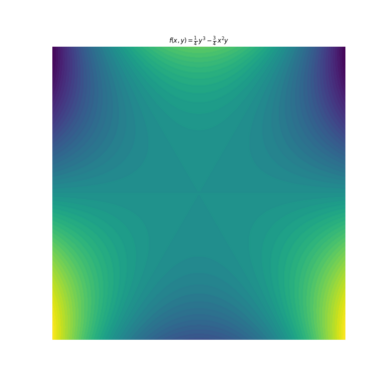Harish-Chandra isomorphism

Short description: Isomorphism of commutative rings constructed in the theory of Lie algebras

In mathematics, the Harish-Chandra isomorphism, introduced by Harish-Chandra (1951), is an isomorphism of commutative rings constructed in the theory of Lie algebras. The isomorphism maps the center [math]\displaystyle{ \mathcal{Z}(U(\mathfrak{g})) }[/math] of the universal enveloping algebra [math]\displaystyle{ U(\mathfrak{g}) }[/math] of a reductive Lie algebra [math]\displaystyle{ \mathfrak{g} }[/math] to the elements [math]\displaystyle{ S(\mathfrak{h})^W }[/math] of the symmetric algebra [math]\displaystyle{ S(\mathfrak{h}) }[/math] of a Cartan subalgebra [math]\displaystyle{ \mathfrak{h} }[/math] that are invariant under the Weyl group [math]\displaystyle{ W }[/math].

Introduction and setting

Let [math]\displaystyle{ \mathfrak{g} }[/math] be a semisimple Lie algebra, [math]\displaystyle{ \mathfrak{h} }[/math] its Cartan subalgebra and [math]\displaystyle{ \lambda, \mu \in \mathfrak{h}^* }[/math] be two elements of the weight space (where [math]\displaystyle{ \mathfrak{h}^* }[/math] is the dual of [math]\displaystyle{ \mathfrak{h} }[/math]) and assume that a set of positive roots [math]\displaystyle{ \Phi_+ }[/math] have been fixed. Let [math]\displaystyle{ V_\lambda }[/math] and [math]\displaystyle{ V_\mu }[/math] be highest weight modules with highest weights [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \mu }[/math] respectively.

Central characters

The [math]\displaystyle{ \mathfrak{g} }[/math]-modules [math]\displaystyle{ V_\lambda }[/math] and [math]\displaystyle{ V_\mu }[/math] are representations of the universal enveloping algebra [math]\displaystyle{ U(\mathfrak{g}) }[/math] and its center acts on the modules by scalar multiplication (this follows from the fact that the modules are generated by a highest weight vector). So, for [math]\displaystyle{ v \in V_\lambda }[/math] and [math]\displaystyle{ x \in \mathcal{Z}(U(\mathfrak{g})) }[/math], [math]\displaystyle{ x\cdot v:=\chi_\lambda(x)v }[/math] and similarly for [math]\displaystyle{ V_\mu }[/math], where the functions [math]\displaystyle{ \chi_\lambda, \,\chi_\mu }[/math] are homomorphisms from [math]\displaystyle{ \mathcal{Z}(U(\mathfrak{g})) }[/math] to scalars called central characters.

Statement of Harish-Chandra theorem

For any [math]\displaystyle{ \lambda, \mu \in \mathfrak{h}^* }[/math], the characters [math]\displaystyle{ \chi_\lambda=\chi_\mu }[/math] if and only if [math]\displaystyle{ \lambda + \delta }[/math] and [math]\displaystyle{ \mu + \delta }[/math] are on the same orbit of the Weyl group of [math]\displaystyle{ \mathfrak{h}^* }[/math], where [math]\displaystyle{ \delta }[/math] is the half-sum of the positive roots, sometimes known as the Weyl vector.

Another closely related formulation is that the Harish-Chandra homomorphism from the center of the universal enveloping algebra [math]\displaystyle{ \mathcal{Z}(U(\mathfrak{g})) }[/math] to [math]\displaystyle{ S(\mathfrak{h})^W }[/math] (the elements of the symmetric algebra of the Cartan subalgebra fixed by the Weyl group) is an isomorphism.

Explicit isomorphism

More explicitly, the isomorphism can be constructed as the composition of two maps, one from [math]\displaystyle{ \mathfrak{Z} = \mathcal{Z}(U(\mathfrak{g})) }[/math] to [math]\displaystyle{ U(\mathfrak{h}) = S(\mathfrak{h}), }[/math] and another from [math]\displaystyle{ S(\mathfrak{h}) }[/math] to itself.

The first is a projection [math]\displaystyle{ \gamma: \mathfrak{Z} \rightarrow S(\mathfrak{h}) }[/math]. For a choice of positive roots [math]\displaystyle{ \Phi_+ }[/math], defining [math]\displaystyle{ n^+ = \bigoplus_{\alpha \in \Phi_+} \mathfrak{g}_\alpha, n^- = \bigoplus_{\alpha \in \Phi_-} \mathfrak{g}_\alpha }[/math] as the corresponding positive nilpotent subalgebra and negative nilpotent subalgebra respectively, due to the Poincaré–Birkhoff–Witt theorem there is a decomposition [math]\displaystyle{ U(\mathfrak{g}) = U(\mathfrak{h}) \oplus (U(\mathfrak{g})\mathfrak{n}^+ + \mathfrak{n}^-U(\mathfrak{g})). }[/math] If [math]\displaystyle{ z \in \mathfrak{Z} }[/math] is central, then in fact [math]\displaystyle{ z \in U(\mathfrak{h}) \oplus (U(\mathfrak{g})\mathfrak{n}^+ \cap \mathfrak{n}^-U(\mathfrak{g})). }[/math] The restriction of the projection [math]\displaystyle{ U(\mathfrak{g}) \rightarrow U(\mathfrak{h}) }[/math] to the centre is [math]\displaystyle{ \gamma: \mathfrak{Z} \rightarrow S(\mathfrak{h}) }[/math], and is a homomorphism of algebras. This is related to the central characters by [math]\displaystyle{ \chi_\lambda(x) = \gamma(x)(\lambda) }[/math]

The second map is the twist map [math]\displaystyle{ \tau: S(\mathfrak{h}) \rightarrow S(\mathfrak{h}) }[/math]. On [math]\displaystyle{ \mathfrak{h} }[/math] viewed as a subspace of [math]\displaystyle{ U(\mathfrak{h}) }[/math] it is defined [math]\displaystyle{ \tau(h) = h - \delta(h)1 }[/math] with [math]\displaystyle{ \delta }[/math] the Weyl vector.

Then [math]\displaystyle{ \tilde \gamma = \tau \circ \gamma: \mathfrak{Z} \rightarrow S(\mathfrak{h}) }[/math] is the isomorphism. The reason this twist is introduced is that [math]\displaystyle{ \chi_\lambda }[/math] is not actually Weyl-invariant, but it can be proven that the twisted character [math]\displaystyle{ \tilde \chi_\lambda = \chi_{\lambda - \delta} }[/math] is.

Applications

The theorem has been used to obtain a simple Lie algebraic proof of Weyl's character formula for finite-dimensional irreducible representations. The proof has been further simplified by Victor Kac, so that only the quadratic Casimir operator is required; there is a corresponding streamlined treatment proof of the character formula in the second edition of (Humphreys 1978).

Further, it is a necessary condition for the existence of a non-zero homomorphism of some highest weight modules (a homomorphism of such modules preserves central character). A simple consequence is that for Verma modules or generalized Verma modules [math]\displaystyle{ V_\lambda }[/math] with highest weight [math]\displaystyle{ \lambda }[/math], there exist only finitely many weights [math]\displaystyle{ \mu }[/math] for which a non-zero homomorphism [math]\displaystyle{ V_\lambda \rightarrow V_\mu }[/math] exists.

Fundamental invariants

For [math]\displaystyle{ \mathfrak{g} }[/math] a simple Lie algebra, let [math]\displaystyle{ r }[/math] be its rank, that is, the dimension of any Cartan subalgebra [math]\displaystyle{ \mathfrak{h} }[/math] of [math]\displaystyle{ \mathfrak{g} }[/math]. H. S. M. Coxeter observed that [math]\displaystyle{ S(\mathfrak{h})^W }[/math] is isomorphic to a polynomial algebra in [math]\displaystyle{ r }[/math] variables (see Chevalley–Shephard–Todd theorem for a more general statement). Therefore, the center of the universal enveloping algebra of a simple Lie algebra is isomorphic to a polynomial algebra. The degrees of the generators of the algebra are the degrees of the fundamental invariants given in the following table.

Lie algebra	Coxeter number h	Dual Coxeter number	Degrees of fundamental invariants
R	0	0	1
An	n + 1	n + 1	2, 3, 4, ..., n + 1
Bn	2n	2n − 1	2, 4, 6, ..., 2n
Cn	2n	n + 1	2, 4, 6, ..., 2n
Dn	2n − 2	2n − 2	n; 2, 4, 6, ..., 2n − 2
E6	12	12	2, 5, 6, 8, 9, 12
E7	18	18	2, 6, 8, 10, 12, 14, 18
E8	30	30	2, 8, 12, 14, 18, 20, 24, 30
F4	12	9	2, 6, 8, 12
G2	6	4	2, 6

The number of the fundamental invariants of a Lie group is equal to its rank. Fundamental invariants are also related to the cohomology ring of a Lie group. In particular, if the fundamental invariants have degrees [math]\displaystyle{ d_1, \cdots, d_r }[/math], then the generators of the cohomology ring have degrees [math]\displaystyle{ 2d_1-1, \cdots, 2d_r-1 }[/math]. Due to this, the degrees of the fundamental invariants can be calculated from the Betti numbers of the Lie group and vice versa. In another direction, fundamental invariants are related to cohomology of the classifying space. The cohomology ring [math]\displaystyle{ H^*(BG, \mathbb{R}) }[/math] is isomorphic to a polynomial algebra on generators with degrees [math]\displaystyle{ 2d_1, \cdots, 2d_r }[/math].

Examples

• If [math]\displaystyle{ \mathfrak{g} }[/math] is the Lie algebra [math]\displaystyle{ \mathfrak{sl}(2, \mathbb{R}) }[/math], then the center of the universal enveloping algebra is generated by the Casimir invariant of degree 2, and the Weyl group acts on the Cartan subalgebra, which is isomorphic to [math]\displaystyle{ \mathbb{R} }[/math], by negation, so the invariant of the Weyl group is the square of the generator of the Cartan subalgebra, which is also of degree 2.
• For [math]\displaystyle{ \mathfrak{g} = A_2 = \mathfrak{sl}(3,\mathbb{C}) }[/math], the Harish-Chandra isomorphism says [math]\displaystyle{ \mathcal{Z}(U(\mathfrak{g})) }[/math] is isomorphic to a polynomial algebra of Weyl-invariant polynomials in two variables [math]\displaystyle{ h_1, h_2 }[/math] (since the Cartan subalgebra is two-dimensional). For [math]\displaystyle{ A_2 }[/math], the Weyl group is [math]\displaystyle{ S_3 \cong D_6 }[/math] which acts on the CSA in the standard representation. Since the Weyl group acts by reflections, they are isometries and so the degree 2 polynomial [math]\displaystyle{ f_2(h_1, h_2) = h_1^2 + h_2^2 }[/math] is Weyl-invariant. The contours of the degree 3 Weyl-invariant polynomial (for a particular choice of standard representation where one of the reflections is across the x-axis) are shown below. These two polynomials generate the polynomial algebra, and are the fundamental invariants for [math]\displaystyle{ A_2 }[/math].
• For all the Lie algebras in the classification, there is a fundamental invariant of degree 2, the quadratic Casimir. In the isomorphism, these correspond to a degree 2 polynomial on the CSA. Since the Weyl group acts by reflections on the CSA, they are isometries, so the degree 2 invariant polynomial is [math]\displaystyle{ f_2(\mathbf{h}) = h_1^2 + \cdots + h_r^2 }[/math] where [math]\displaystyle{ r }[/math] is the dimension of the CSA [math]\displaystyle{ \mathfrak{h} }[/math], also known as the rank of the Lie algebra.
• For [math]\displaystyle{ \mathfrak{g} = A_1 = \mathfrak{sl}(2, \mathbb{C}) }[/math], the Cartan subalgebra is one-dimensional, and the Harish-Chandra isomorphism says [math]\displaystyle{ \mathcal{Z}(U(\mathfrak{g})) }[/math] is isomorphic to the algebra of Weyl-invariant polynomials in a single variable [math]\displaystyle{ h }[/math]. The Weyl group is [math]\displaystyle{ S_2 }[/math] acting as reflection, with non-trivial element acting on polynomials by [math]\displaystyle{ h \mapsto -h }[/math]. The subalgebra of Weyl-invariant polynomials in the full polynomial algebra [math]\displaystyle{ K[h] }[/math] is therefore only the even polynomials, generated by [math]\displaystyle{ f_2(h) = h^2 }[/math].

Weyl-invariant cubic for A₂, corresponding to the degree 3 fundamental invariant

• For [math]\displaystyle{ \mathfrak{g} = B_2 = \mathfrak{so}(5) = \mathfrak{sp}(4) }[/math], the Weyl group is [math]\displaystyle{ D_8 }[/math], acting on two coordinates [math]\displaystyle{ h_1, h_2 }[/math], and is generated (non-minimally) by four reflections, which act on coordinates as [math]\displaystyle{ (h_1 \mapsto -h_1, h_2 \mapsto h_2), (h_1 \mapsto h_1, h_2 \mapsto -h_2), (h_1 \mapsto h_2, h_2 \mapsto h_1), (h_1 \mapsto -h_2, h_2 \mapsto h_1) }[/math]. Any invariant quartic must be even in both [math]\displaystyle{ h_1 }[/math] and [math]\displaystyle{ h_2 }[/math], and invariance under exchange of coordinates means any invariant quartic can be written [math]\displaystyle{ f_4(h_1, h_2) = ah_1^4 + bh_1^2h_2^2 + ah_2^4. }[/math] Despite this being a two-dimensional vector space, this contributes only one new fundamental invariant as [math]\displaystyle{ f_2(h_1,h_2)^2 }[/math] lies in the space. In this case, there is no unique choice of quartic invariant as any polynomial with [math]\displaystyle{ b \neq 2a }[/math] (and [math]\displaystyle{ a,b }[/math] not both zero) suffices.

Generalization to affine Lie algebras

The above result holds for reductive, and in particular semisimple Lie algebras. There is a generalization to affine Lie algebras shown by Feigin and Frenkel showing that an algebra known as the Feigin–Frenkel center is isomorphic to a W-algebra associated to the Langlands dual Lie algebra [math]\displaystyle{ ^L\mathfrak{g} }[/math].

The Feigin–Frenkel center of an affine Lie algebra [math]\displaystyle{ \hat \mathfrak{g} }[/math] is not exactly the center of the universal enveloping algebra [math]\displaystyle{ \mathcal{Z}(U(\hat \mathfrak{g})) }[/math]. They are elements [math]\displaystyle{ S }[/math] of the vacuum affine vertex algebra at critical level [math]\displaystyle{ k = -h^\vee }[/math], where [math]\displaystyle{ h^\vee }[/math] is the dual Coxeter number for [math]\displaystyle{ \mathfrak{g} }[/math] which are annihilated by the positive loop algebra [math]\displaystyle{ \mathfrak{g}[t] }[/math] part of [math]\displaystyle{ \hat \mathfrak{g} }[/math], that is, [math]\displaystyle{ \mathfrak{Z}(\hat \mathfrak{g}) := \{S \in V_{\text{cri}}(\mathfrak{g}) | \mathfrak{g}[t]S = 0\} }[/math] where [math]\displaystyle{ V_{\text{cri}}(\mathfrak{g}) }[/math] is the affine vertex algebra at the critical level. Elements of this center are also known as singular vectors or Segal–Sugawara vectors.

The isomorphism in this case is an isomorphism between the Feigin–Frenkel center and the W-algebra constructed associated to the Langlands dual Lie algebra by Drinfeld–Sokolov reduction: [math]\displaystyle{ \mathfrak{Z}(\hat \mathfrak{g}) \cong \mathcal{W}(^L\mathfrak{g}). }[/math] There is also a description of [math]\displaystyle{ \mathfrak{Z}(\hat \mathfrak{g}) }[/math] as a polynomial algebra in a finite number of countably infinite families of generators, [math]\displaystyle{ \partial^n S_i, i = 1, \cdots, l, n \geq 0 }[/math], where [math]\displaystyle{ S_i, i = 1, \cdots, l }[/math] have degrees [math]\displaystyle{ d_i +1, i = 1, \cdots, l }[/math] and [math]\displaystyle{ \partial }[/math] is the (negative of) the natural derivative operator on the loop algebra.

See also

• Translation functor
• Infinitesimal character

External resources

Notes on the Harish-Chandra isomorphism

References

• Harish-Chandra (1951), "On some applications of the universal enveloping algebra of a semisimple Lie algebra", Transactions of the American Mathematical Society 70 (1): 28–96, doi:10.2307/1990524 
• Humphreys, James E. (1978). Introduction to Lie algebras and representation theory. Graduate Texts in Mathematics. 9 (Second revised ed.). Springer-Verlag. ISBN 0-387-90053-5.  (Contains an improved proof of Weyl's character formula.)
• Humphreys, James E. (2008), Representations of semisimple Lie algebras in the BGG category O, AMS, p. 26, ISBN 978-0-8218-4678-0 
• Knapp, Anthony W.; Vogan, David A. (1995), Cohomological induction and unitary representations, Princeton Mathematical Series, 45, Princeton University Press, ISBN 978-0-691-03756-1 
• Knapp, Anthony W. (2013), "V. Finite Dimensional Representations §5. Harish-Chandra Isomorphism", Lie Groups Beyond an Introduction, Progress in Mathematics, 140, Springer, pp. 246–258, ISBN 978-1-4757-2453-0, https://books.google.com/books?id=J8EGCAAAQBAJ&pg=PA246