Heawood number

Short description: Upper bound for number of colors that suffice to color any graph

In mathematics, the Heawood number of a surface is an upper bound for the number of colors that suffice to color any graph embedded in the surface.

In 1890 Heawood proved for all surfaces except the sphere that no more than

[math]\displaystyle{ H(S)=\left\lfloor\frac{7+\sqrt{49-24 e(S)}}{2}\right\rfloor = \left\lfloor\frac{7+\sqrt{1+48 g(S)}}{2}\right\rfloor }[/math]

colors are needed to color any graph embedded in a surface of Euler characteristic [math]\displaystyle{ e(S) }[/math], or genus [math]\displaystyle{ g(S) }[/math] for an orientable surface. The number [math]\displaystyle{ H(S) }[/math] became known as Heawood number in 1976.

A 6-colored Klein bottle, the only exception to the Heawood conjecture

Franklin proved that the chromatic number of a graph embedded in the Klein bottle can be as large as [math]\displaystyle{ 6 }[/math], but never exceeds [math]\displaystyle{ 6 }[/math]. Later it was proved in the works of Gerhard Ringel, J. W. T. Youngs, and other contributors that the complete graph with [math]\displaystyle{ H(S) }[/math] vertices can be embedded in the surface [math]\displaystyle{ S }[/math] unless [math]\displaystyle{ S }[/math] is the Klein bottle. This established that Heawood's bound could not be improved.

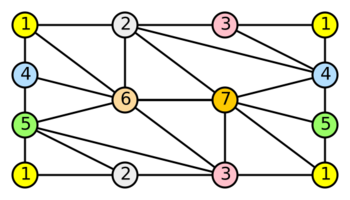
For example, the complete graph on [math]\displaystyle{ 7 }[/math] vertices can be embedded in the torus as follows:

The case of the sphere is the four-color conjecture, which was settled by Kenneth Appel and Wolfgang Haken in 1976.

Notes

• Béla Bollobás, Graph Theory: An Introductory Course, Graduate Texts in Mathematics, volume 63, Springer-Verlag, 1979. Zbl 0411.05032.
• Thomas L. Saaty and Paul Chester Kainen; The Four-Color Problem: Assaults and Conquest, Dover, 1986. Zbl 0463.05041.