Hick's law

From HandWiki

Hick's law, or the Hick–Hyman law, named after British and American psychologists William Edmund Hick and Ray Hyman, describes the time it takes for a person to make a decision as a result of the possible choices: increasing the number of choices will increase the decision time logarithmically. The Hick–Hyman law assesses cognitive information capacity in choice reaction experiments. The amount of time taken to process a certain amount of bits in the Hick–Hyman law is known as the "rate of gain of information". The plain language implication of the finding is that increasing the number of choices does not directly increase the time to choose. In other words, twice as many choices does not result in twice as long to choose. Also, because the relationship is logarithmic, the increase in time it takes to choose becomes less and less as the number of choices increases.

Background

In 1868, Franciscus Donders reported the relationship between having multiple stimuli and choice reaction time. In 1885, J. Merkel discovered that the response time is longer when a stimulus belongs to a larger set of stimuli. Psychologists began to see similarities between this phenomenon and information theory.[who?]

Hick first began experimenting with this theory in 1951.[1] In his first experiment, there were 10 lamps arranged circularly around the subject. There were 10 Morse keys for each of his fingers that corresponded to these lamps. A running pre-punched tape roll activated a random lamp every 5 seconds; 4 electric pens recorded this lamp activation on moving paper in 4-bit binary. When the subject tapped the corresponding key, the 4 pens recorded the response, using the same system. Although Hicks notes his experimental design using a 4-bit binary recording process was capable of showing up to 15 positions and "all clear", in his experiment he required the device to give an accurate record of reaction time between 10 options after a stimulus for the experiment.

Hick performed a second experiment using the same task, while keeping the number of alternatives at 10. The participant performed the task the first two times with the instruction to perform the task as accurately as possible. For the last task, the participant was asked to perform the task as quickly as possible.

While Hick was stating that the relationship between reaction time and the number of choices was logarithmic, Hyman wanted to better understand the relationship between the reaction time and the mean number of choices. In Hyman’s experiment, he had eight different lights arranged in a 6x6 matrix.[2] Each of these different lights was given a name, so the participant was timed in the time it took to say the name of the light after it was lit. Further experiments changed the number of each different type of light. Hyman was responsible for determining a linear relation between reaction time and the information transmitted.

Law

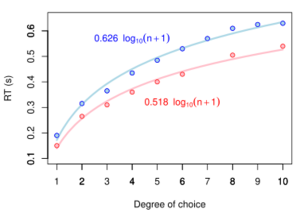
Data from W. E. Hick (1952) demonstrating Hick's Law: The relationship between reaction time and number of response options across two participants (red and blue).

Given n equally probable choices, the average reaction time T required to choose among the choices is approximately:

[math]\displaystyle{ T = b \cdot \log_{2}(n + 1) }[/math]

where b is a constant that can be determined empirically by fitting a line to measured data. The logarithm expresses depth of "choice tree" hierarchy – log2 indicates binary search was performed. Addition of 1 to n takes into account the "uncertainty about whether to respond or not, as well as about which response to make."[3]

In the case of choices with unequal probabilities, the law can be generalized as:

[math]\displaystyle{ T = b H }[/math]

where H is strongly related to the information-theoretic entropy of the decision, defined as

[math]\displaystyle{ H = \sum_i^n p_i \log_{2}(1/p_i + 1) }[/math]

where pi refers to the probability of the ith alternative yielding the information-theoretic entropy.

Hick's law is similar in form to Fitts's law. Hick's law has a logarithmic form because people subdivide the total collection of choices into categories, eliminating about half of the remaining choices at each step, rather than considering each and every choice one-by-one, which would require linear time.

Relation to IQ

Roth's application of Hick's law
"Bit" is the unit of log2(n).

E. Roth (1964) demonstrated a correlation between IQ and information processing speed, which is the reciprocal of the slope of the function:[4]

[math]\displaystyle{ \text{Reaction Time} = \text{Movement Time} + \frac{ \log_{2}(n) } {\text{Processing Speed} } }[/math]

where n is the number of choices. The time it takes to come to a decision is:

proportional to :[math]\displaystyle{ \frac{ \log_{2}(n) } {\text{Processing Speed}} }[/math]

Stimulus–response compatibility

The stimulus–response compatibility is known to also affect the choice reaction time for the Hick–Hyman law. This means that the response should be similar to the stimulus itself (such as turning a steering wheel to turn the wheels of the car). The action the user performs is similar to the response the driver receives from the car.

Exceptions

The sigmoid function remains a better representation than the linear function of the relationship between predictability and reaction time.

Studies suggest that the search for a word within a randomly ordered list—in which the reaction time increases linearly according to the number of items—does not allow for the generalization of the scientific law, considering that, in other conditions, the reaction time may not be linearly associated to the logarithm of the number of elements or even show other variations of the basic plane.

Exceptions to Hick's law have been identified in studies of verbal response to familiar stimuli, where there is no relationship or only a subtle increase in the reaction time associated with an increased number of elements,[5] and saccade responses, where it was shown that there is either no relationship,[6] or a decrease in the saccadic time with the increase of the number of elements, thus an antagonistic effect to that postulated by Hick's law.[7]

The generalization of Hick's law was also tested in studies on the predictability of transitions associated with the reaction time of elements that appeared in a structured sequence.[8][9] This process was first described as being in accordance to Hick's law,[10] but more recently it was shown that the relationship between predictability and reaction time is sigmoid, not linear associated with different modes of action.[11]

Hick's law is sometimes cited to justify menu design decisions. For example, to find a given word (e.g. the name of a command) in a randomly ordered word list (e.g. a menu), scanning of each word in the list is required, consuming linear time, so Hick's law does not apply. However, if the list is alphabetical and the user knows the name of the command, he or she may be able to use a subdividing strategy that works in logarithmic time.[12]

See also

Notes

  1. ↑ Hick, W.E. (1952). "On the rate of gain of information". Quarterly Journal of Experimental Psychology 4 (1): 11–26. doi:10.1080/17470215208416600. http://www2.psychology.uiowa.edu/faculty/mordkoff/InfoProc/pdfs/Hick%201952.pdf. 
  2. ↑ Hyman, R (March 1953). "Stimulus information as a determinant of reaction time". Journal of Experimental Psychology 45 (3): 188–96. doi:10.1037/h0056940. PMID 13052851. 
  3. ↑ Card, Stuart K.; Moran, Thomas P.; Newell, A. (1983). The Psychology of Human–Computer Interaction. Hilldale, London: Lawrence Erlbaum. 
  4. ↑ Roth, Erwin (1964). "Die Geschwindigkeit der Verarbeitung von Information und ihr Zusammenhang mit Intelligenz" (in de). Zeitschrift für Experimentelle und Angewandte Psychologie 11: 616–622. 
  5. ↑ Longstreth, L. E.; El-Zahhar, N.; Alcorn, M. B. (1985). "Exceptions to Hick's Law: Explorations With a Response Duration Measure" (in en). Journal of Experimental Psychology: General 114 (4): 417–434. doi:10.1037/0096-3445.114.4.417. PMID 2934496. 
  6. ↑ Kveraga, K.; Boucher, L.; Hughes, H. C. (2002). "Saccades operate in Violation of Hick's law" (in en). Experimental Brain Research 146 (3): 307–314. doi:10.1007/s00221-002-1168-8. PMID 12232687. 
  7. ↑ Lawrence, B. M.; St. John, A.; Abrams, R. A.; Snyder, L. H. (2008). "An anti-Hick's effect in monkey and human saccade reaction times" (in en). Journal of Vision 8 (26): 26.1–7. doi:10.1167/8.3.26. PMID 18484832. 
  8. ↑ Stadler, M. A. (1992). "Statistical Structure and Implicit Learning Serial" (in en). Journal of Experimental Psychology: Learning, Memory, and Cognition 18 (2): 318–327. doi:10.1037/0278-7393.18.2.318. 
  9. ↑ Remillard, G.; Clark (2001). "Implicit Learning of First-, second-, and Third-Order Transition Probabilities" (in en). Journal of Experimental Psychology: Learning, Memory, and Cognition 27 (2): 483–498. doi:10.1037/0278-7393.27.2.483. PMID 11294445. 
  10. ↑ Jamieson, R. K.; Mewhort (2009). "Applying an exemplary model to the serial reaction-time task: Anticipating from experience" (in en). The Quarterly Journal of Experimental Psychology 62 (9): 1757–1783. doi:10.1080/17470210802557637. PMID 19219752. 
  11. ↑ Pavão, R.; Savietto, J.P.; Sato, J.R.; Xavier, G. F.; Helene, A. F. (2016). "On Sequence Learning Models: Open-loop Control Not Strictly Guided by Hick's Law" (in en). Scientific Reports 6: 23018. doi:10.1038/srep23018. PMID 26975409. Bibcode: 2016NatSR...623018P. 
  12. ↑ Landauer, T. K.; Nachbar, D. W. (1985). "Selection from alphabetic and numeric menu trees using a touch screen". Proceedings of the SIGCHI conference on Human factors in computing systems - CHI '85. pp. 73. doi:10.1145/317456.317470. ISBN 978-0897911498. 

References

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Hick%27s_law&oldid=3361777"