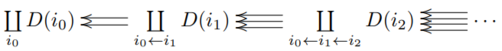Homotopy colimit

In mathematics, especially in algebraic topology, the homotopy limit and colimit^{pg 52} are variants of the notions of limit and colimit extended to the homotopy category [math]\displaystyle{ \text{Ho}(\textbf{Top}) }[/math]. The main idea is this: if we have a diagram

[math]\displaystyle{ F: I \to \textbf{Top} }[/math]

considered as an object in the homotopy category of diagrams [math]\displaystyle{ F \in \text{Ho}(\textbf{Top}^I) }[/math], (where the homotopy equivalence of diagrams is considered pointwise), then the homotopy limit and colimits then correspond to the cone and cocone

[math]\displaystyle{ \begin{align} \underset{\leftarrow I}{\text{Holim}}(F)&: * \to \textbf{Top}\\ \underset{\rightarrow I}{\text{Hocolim}}(F)&: * \to \textbf{Top} \end{align} }[/math]

which are objects in the homotopy category [math]\displaystyle{ \text{Ho}(\textbf{Top}^*) }[/math], where [math]\displaystyle{ * }[/math] is the category with one object and one morphism. Note this category is equivalent to the standard homotopy category [math]\displaystyle{ \text{Ho}(\textbf{Top}) }[/math] since the latter homotopy functor category has functors which picks out an object in [math]\displaystyle{ \text{Top} }[/math] and a natural transformation corresponds to a continuous function of topological spaces. Note this construction can be generalized to model categories, which give techniques for constructing homotopy limits and colimits in terms of other homotopy categories, such as derived categories. Another perspective formalizing these kinds of constructions are derivators^{pg 193} which are a new framework for homotopical algebra.

Introductory examples

Homotopy pushout

The concept of homotopy colimit^{pg 4-8} is a generalization of homotopy pushouts, such as the mapping cylinder used to define a cofibration. This notion is motivated by the following observation: the (ordinary) pushout

[math]\displaystyle{ D^n \sqcup_{S^{n-1}} pt }[/math]

is the space obtained by contracting the n-1-sphere (which is the boundary of the n-dimensional disk) to a single point. This space is homeomorphic to the n-sphere Sⁿ. On the other hand, the pushout

[math]\displaystyle{ pt \sqcup_{S^{n-1}} pt }[/math]

is a point. Therefore, even though the (contractible) disk Dⁿ was replaced by a point, (which is homotopy equivalent to the disk), the two pushouts are not homotopy (or weakly) equivalent.

Therefore, the pushout is not well-aligned with a principle of homotopy theory, which considers weakly equivalent spaces as carrying the same information: if one (or more) of the spaces used to form the pushout is replaced by a weakly equivalent space, the pushout is not guaranteed to stay weakly equivalent. The homotopy pushout rectifies this defect.

The homotopy pushout of two maps [math]\displaystyle{ A \leftarrow B \rightarrow C }[/math] of topological spaces is defined as

[math]\displaystyle{ A \sqcup_1 B \times [0,1] \sqcup_0 B \sqcup_1 B \times [0,1] \sqcup_0 C }[/math],

i.e., instead of glueing B in both A and C, two copies of a cylinder on B are glued together and their ends are glued to A and C. For example, the homotopy colimit of the diagram (whose maps are projections)

[math]\displaystyle{ X_0 \leftarrow X_0 \times X_1 \rightarrow X_1 }[/math]

is the join [math]\displaystyle{ X_0 * X_1 }[/math].

It can be shown that the homotopy pushout does not share the defect of the ordinary pushout: replacing A, B and / or C by a homotopic space, the homotopy pushout will also be homotopic. In this sense, the homotopy pushouts treats homotopic spaces as well as the (ordinary) pushout does with homeomorphic spaces.

Composition of maps

Another useful and motivating examples of a homotopy colimit is constructing models for the homotopy colimit of the diagram

[math]\displaystyle{ A \xrightarrow{f} X \xrightarrow{g} Y }[/math]

of topological spaces. There are a number of ways to model this colimit: the first is to consider the space

[math]\displaystyle{ \left[ (A\times I)\coprod (X\times I) \coprod Y \right] / \sim }[/math]

where [math]\displaystyle{ \sim }[/math] is the equivalence relation identifying

[math]\displaystyle{ \begin{align} (a,1) &\sim (f(a),0) \\ (x,1) &\sim g(x) \end{align} }[/math]

which can pictorially be described as the picture

Because we can similarly interpret the diagram above as the commutative diagram, from properties of categories, we get a commutative diagram

frameless|117x117px

giving a homotopy colimit. We could guess this looks like

frameless|206x206px

but notice we have introduced a new cycle to fill in the new data of the composition. This creates a technical problem which can be solved using simplicial techniques: giving a method for constructing a model for homotopy colimits. The new diagram, forming the homotopy colimit of the composition diagram pictorially is represented as

giving another model of the homotopy colimit which is homotopy equivalent to the original diagram (without the composition of [math]\displaystyle{ g\circ f }[/math]) given above.

Mapping telescope

The homotopy colimit of a sequence of spaces

[math]\displaystyle{ X_1 \to X_2 \to \cdots, }[/math]

is the mapping telescope. One example computation is taking the homotopy colimit of a sequence of cofibrations. The colimit of ^{pg 62} this diagram gives a homotopy colimit. This implies we could compute the homotopy colimit of any mapping telescope by replacing the maps with cofibrations.

General definition

Homotopy limit

Treating examples such as the mapping telescope and the homotopy pushout on an equal footing can be achieved by considering an I-diagram of spaces, where I is some "indexing" category. This is a functor

[math]\displaystyle{ X: I \to Spaces, }[/math]

i.e., to each object i in I, one assigns a space X_i and maps between them, according to the maps in I. The category of such diagrams is denoted Spaces^I.

There is a natural functor called the diagonal,

[math]\displaystyle{ \Delta_0: Spaces \to Spaces^I }[/math]

which sends any space X to the diagram which consists of X everywhere (and the identity of X as maps between them). In (ordinary) category theory, the right adjoint to this functor is the limit. The homotopy limit is defined by altering this situation: it is the right adjoint to

[math]\displaystyle{ \Delta: Spaces \to Spaces^I }[/math]

which sends a space X to the I-diagram which at some object i gives

[math]\displaystyle{ X \times |N(I / i)| }[/math]

Here I/i is the slice category (its objects are arrows j → i, where j is any object of I), N is the nerve of this category and |-| is the topological realization of this simplicial set.

Homotopy colimit

Similarly, one can define a colimit as the left adjoint to the diagonal functor Δ₀ given above. To define a homotopy colimit, we must modify Δ₀ in a different way. A homotopy colimit can be defined as the left adjoint to a functor Δ : Spaces → Spaces^I where

Δ(X)(i) = Hom_Spaces (‹See Tfd›|N(I^op /i)|, X),

where I^op is the opposite category of I. Although this is not the same as the functor Δ above, it does share the property that if the geometric realization of the nerve category (‹See Tfd›|N(-)|) is replaced with a point space, we recover the original functor Δ₀.

Construction of colimits with simplicial replacements

Given a small category [math]\displaystyle{ I }[/math] and a diagram [math]\displaystyle{ D:I \to \textbf{Top} }[/math], we can construct the homotopy colimit using a simplicial replacement of the diagram. This is a simplicial space, [math]\displaystyle{ \text{srep}(D)_\bullet }[/math] given by the diagram^{pg 16-17}

where

[math]\displaystyle{ \text{srep}(D)_n = \underset{i_0 \leftarrow i_1 \leftarrow \cdots \leftarrow i_n}{\coprod}D(i_n) }[/math]

given by chains of composable maps in the indexing category [math]\displaystyle{ I }[/math]. Then, the homotopy colimit of [math]\displaystyle{ D }[/math] can be constructed as the geometric realization of this simplicial space, so

[math]\displaystyle{ \underset{\to}{\text{hocolim}}D = |\text{srep}(D)_\bullet| }[/math]

Notice that this agrees with the picture given above for the composition diagram of [math]\displaystyle{ A \to X \to Y }[/math].

Relation to the (ordinary) colimit and limit

There is always a map

[math]\displaystyle{ \mathrm{hocolim} X_i \to \mathrm{colim} X_i. }[/math]

Typically, this map is not a weak equivalence. For example, the homotopy pushout encountered above always maps to the ordinary pushout. This map is not typically a weak equivalence, for example the join is not weakly equivalent to the pushout of [math]\displaystyle{ X_0 \leftarrow X_0 \times X_1 \rightarrow X_1 }[/math], which is a point.

Further examples and applications

Just as limit is used to complete a ring, holim is used to complete a spectrum.

See also

• Derivator
• Homotopy fiber
• Homotopy cofiber
• Cohomology of categories
• Spectral sequence of homotopy colimits

References

• A Primer on Homotopy Colimits
• Homotopy colimits in the category of small categories
• Categories and Orbispaces
• Hatcher, Allen (2002), Algebraic Topology, Cambridge: Cambridge University Press, ISBN 0-521-79540-0, http://www.math.cornell.edu/~hatcher/AT/ATpage.html .

Further reading

• Homotopy limit-colimit diagrams in stable model categories
• pg.80 Homotopy Colimits and Limits