Join (topology)

Geometric join of two line segments. The original spaces are shown in green and blue. The join is a three-dimensional solid, a disphenoid, in gray.

In topology, a field of mathematics, the join of two topological spaces $A$ and $B$, often denoted by $A\ast B$ or $A\star B$, is a topological space formed by taking the disjoint union of the two spaces, and attaching line segments joining every point in $A$ to every point in $B$. The join of a space $A$ with itself is denoted by $A^{\star 2}:=A\star A$. The join is defined in slightly different ways in different contexts

Geometric sets

If

$A$

and

$B$

are subsets of the Euclidean space

${\mathbb{ℝ}}^n$

, then:

$A\star B:=\{t\cdot a+(1-t)\cdot b|a\in A,b\in B,t\in [0,1]\}$

,

that is, the set of all line-segments between a point in

$A$

and a point in

$B$

.

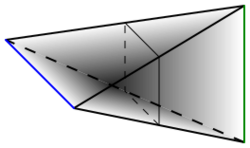
Some authors restrict the definition to subsets that are joinable: any two different line-segments, connecting a point of A to a point of B, meet in at most a common endpoint (that is, they do not intersect in their interior). Every two subsets can be made "joinable". For example, if $A$ is in ${\mathbb{ℝ}}^n$ and $B$ is in ${\mathbb{ℝ}}^m$, then $A\times \{0^m\}\times \{0\}$ and $\{0^n\}\times B\times \{1\}$ are joinable in ${\mathbb{ℝ}}^{n+m+1}$. The figure above shows an example for m=n=1, where $A$ and $B$ are line-segments.

Examples

• The join of two simplices is a simplex: the join of an n-dimensional and an m-dimensional simplex is an (m+n+1)-dimensional simplex. Some special cases are:
  • The join of two disjoint points is an interval (m=n=0).
  • The join of a point and an interval is a triangle (m=0, n=1).
  • The join of two line segments is homeomorphic to a solid tetrahedron or disphenoid, illustrated in the figure above right (m=n=1).
  • The join of a point and an (n-1)-dimensional simplex is an n-dimensional simplex.
• The join of a point and a polygon (or any polytope) is a pyramid, like the join of a point and square is a square pyramid. The join of a point and a cube is a cubic pyramid.
• The join of a point and a circle is a cone, and the join of a point and a sphere is a hypercone.

Topological spaces

If $A$ and $B$ are any topological spaces, then:

$A\star B:=A{\bigsqcup }_{p_0}(A\times B\times [0,1]){\bigsqcup }_{p_1}B,$

where the cylinder $A\times B\times [0,1]$ is attached to the original spaces $A$ and $B$ along the natural projections of the faces of the cylinder:

$A\times B\times \{0\}\stackrel{p_0}{\to }A,$

$A\times B\times \{1\}\stackrel{p_1}{\to }B.$

Usually it is implicitly assumed that $A$ and $B$ are non-empty, in which case the definition is often phrased a bit differently: instead of attaching the faces of the cylinder $A\times B\times [0,1]$ to the spaces $A$ and $B$, these faces are simply collapsed in a way suggested by the attachment projections $p_1,p_2$: we form the quotient space

$A\star B:=(A\times B\times [0,1])/\sim ,$

where the equivalence relation $\sim$ is generated by

$(a,b_1,0)\sim (a,b_2,0)\text{for all }a\in A\text{ and }{b}_1,b_2\in B,$

$(a_1,b,1)\sim (a_2,b,1)\text{for all }{a}_1,a_2\in A\text{ and }b\in B.$

At the endpoints, this collapses $A\times B\times \{0\}$ to $A$ and $A\times B\times \{1\}$ to $B$.

If

$A$

and

$B$

are bounded subsets of the Euclidean space

${\mathbb{ℝ}}^n$

, and

$A\subseteq U$

and

$B\subseteq V$

, where

$U,V$

are disjoint subspaces of

${\mathbb{ℝ}}^n$

such that the dimension of their affine hull is

$dimU+dimV+1$

(e.g. two non-intersecting non-parallel lines in

${\mathbb{ℝ}}^3$

), then the topological definition reduces to the geometric definition, that is, the "geometric join" is homeomorphic to the "topological join":

$((A\times B\times [0,1])/\sim )\simeq \{t\cdot a+(1-t)\cdot b|a\in A,b\in B,t\in [0,1]\}$

Abstract simplicial complexes

If $A$ and $B$ are any abstract simplicial complexes, then their join is an abstract simplicial complex defined as follows:

• The vertex set $V(A\star B)$ is a disjoint union of $V(A)$ and $V(B)$.
• The simplices of $A\star B$ are all disjoint unions of a simplex of $A$ with a simplex of $B$: $A\star B:=\{a\bigsqcup b:a\in A,b\in B\}$ (in the special case in which $V(A)$ and $V(B)$ are disjoint, the join is simply $\{a\cup b:a\in A,b\in B\}$).

Examples

• Suppose $A=\{\mathrm{\varnothing },\{a\}\}$ and $B=\{\mathrm{\varnothing },\{b\}\}$, that is, two sets with a single point. Then $A\star B=\{\mathrm{\varnothing },\{a\},\{b\},\{a,b\}\}$, which represents a line-segment. Note that the vertex sets of A and B are disjoint; otherwise, we should have made them disjoint. For example, $A^{\star 2}=A\star A=\{\mathrm{\varnothing },\{a_1\},\{a_2\},\{a_1,a_2\}\}$ where a₁ and a₂ are two copies of the single element in V(A). Topologically, the result is the same as $A\star B$ - a line-segment.
• Suppose $A=\{\mathrm{\varnothing },\{a\}\}$ and $B=\{\mathrm{\varnothing },\{b\},\{c\},\{b,c\}\}$. Then $A\star B=P(\{a,b,c\})$, which represents a triangle.
• Suppose $A=\{\mathrm{\varnothing },\{a\},\{b\}\}$ and $B=\{\mathrm{\varnothing },\{c\},\{d\}\}$, that is, two sets with two discrete points. then $A\star B$ is a complex with facets $\{a,c\},\{b,c\},\{a,d\},\{b,d\}$, which represents a "square".

The combinatorial definition is equivalent to the topological definition in the following sense: for every two abstract simplicial complexes $A$ and $B$, $||A\star B||$ is homeomorphic to $||A||\star ||B||$, where $||X||$ denotes any geometric realization of the complex $X$.

Maps

Given two maps

$f:A_1\to A_2$

and

$g:B_1\to B_2$

, their join

$f\star g:A_1\star B_1\to A_2\star B_2$

is defined based on the representation of each point in the join

$A_1\star B_1$

as

$t\cdot a+(1-t)\cdot b$

, for some

$a\in A_1,b\in B_1$

:

$f\star g(t\cdot a+(1-t)\cdot b)=t\cdot f(a)+(1-t)\cdot f(b)$

Special cases

The cone of a topological space $X$, denoted $CX$ , is a join of $X$ with a single point.

The suspension of a topological space $X$, denoted $SX$ , is a join of $X$ with $S^0$ (the 0-dimensional sphere, or, the discrete space with two points).

Properties

Commutativity

The join of two spaces is commutative up to homeomorphism, i.e. $A\star B\cong B\star A$.

Associativity

It is not true that the join operation defined above is associative up to homeomorphism for arbitrary topological spaces. However, for locally compact Hausdorff spaces $A,B,C$ we have $(A\star B)\star C\cong A\star (B\star C).$ Therefore, one can define the k-times join of a space with itself, $A^{*k}:=A*\cdots *A$ (k times).

It is possible to define a different join operation $A\hat{\star }B$ which uses the same underlying set as $A\star B$ but a different topology, and this operation is associative for all topological spaces. For locally compact Hausdorff spaces $A$ and $B$, the joins $A\star B$ and $A\hat{\star }B$ coincide.

Homotopy equivalence

If $A$ and $A^{\prime }$ are homotopy equivalent, then $A\star B$ and $A^{\prime }\star B$ are homotopy equivalent too.

Reduced join

Given basepointed CW complexes $(A,a_0)$ and $(B,b_0)$, the "reduced join"

$\frac{A\star B}{A\star \{b_0\}\cup \{a_0\}\star B}$

is homeomorphic to the reduced suspension

$\mathrm{\Sigma }(A\wedge B)$

of the smash product. Consequently, since

$A\star \{b_0\}\cup \{a_0\}\star B$

is contractible, there is a homotopy equivalence

$A\star B\simeq \mathrm{\Sigma }(A\wedge B).$

This equivalence establishes the isomorphism ${\tilde{H}}_n(A\star B)\cong H_{n-1}(A\wedge B)(=H_{n-1}(A\times B/A\vee B))$.

Homotopical connectivity

Given two triangulable spaces $A,B$, the homotopical connectivity (${\eta }_{\pi }$) of their join is at least the sum of connectivities of its parts:

• ${\eta }_{\pi }(A*B)\ge {\eta }_{\pi }(A)+{\eta }_{\pi }(B)$.

As an example, let $A=B=S^0$ be a set of two disconnected points. There is a 1-dimensional hole between the points, so ${\eta }_{\pi }(A)={\eta }_{\pi }(B)=1$. The join $A*B$ is a square, which is homeomorphic to a circle that has a 2-dimensional hole, so ${\eta }_{\pi }(A*B)=2$. The join of this square with a third copy of $S^0$ is a octahedron, which is homeomorphic to $S^2$ , whose hole is 3-dimensional. In general, the join of n copies of $S^0$ is homeomorphic to $S^{n-1}$ and ${\eta }_{\pi }(S^{n-1})=n$.

Deleted join

The deleted join of an abstract complex A is an abstract complex containing all disjoint unions of disjoint faces of A:

$A_{\mathrm{\Delta }}^{*2}:=\{a_1\bigsqcup a_2:a_1,a_2\in A,a_1\cap a_2=\mathrm{\varnothing }\}$

Examples

• Suppose $A=\{\mathrm{\varnothing },\{a\}\}$ (a single point). Then $A_{\mathrm{\Delta }}^{*2}:=\{\mathrm{\varnothing },\{a_1\},\{a_2\}\}$, that is, a discrete space with two disjoint points (recall that $A^{\star 2}=\{\mathrm{\varnothing },\{a_1\},\{a_2\},\{a_1,a_2\}\}$ = an interval).
• Suppose $A=\{\mathrm{\varnothing },\{a\},\{b\}\}$ (two points). Then $A_{\mathrm{\Delta }}^{*2}$ is a complex with facets $\{a_1,b_2\},\{a_2,b_1\}$ (two disjoint edges).
• Suppose $A=\{\mathrm{\varnothing },\{a\},\{b\},\{a,b\}\}$ (an edge). Then $A_{\mathrm{\Delta }}^{*2}$ is a complex with facets $\{a_1,b_1\},\{a_1,b_2\},\{a_2,b_1\},\{a_2,b_2\}$ (a square). Recall that $A^{\star 2}$ represents a solid tetrahedron.
• Suppose A represents an (n-1)-dimensional simplex (with n vertices). Then the join $A^{\star 2}$ is a (2n-1)-dimensional simplex (with 2n vertices): it is the set of all points (x₁,...,x_2n) with non-negative coordinates such that x₁+...+x_2n=1. The deleted join $A_{\mathrm{\Delta }}^{*2}$ can be regarded as a subset of this simplex: it is the set of all points (x₁,...,x_2n) in that simplex, such that the only nonzero coordinates are some k coordinates in x₁,..,x_n, and the complementary n-k coordinates in x_n+1,...,x_2n.

Properties

The deleted join operation commutes with the join. That is, for every two abstract complexes A and B:

$(A*B{)}_{\mathrm{\Delta }}^{*2}=(A_{\mathrm{\Delta }}^{*2})*(B_{\mathrm{\Delta }}^{*2})$

Proof. Each simplex in the left-hand-side complex is of the form

$(a_1\bigsqcup b_1)\bigsqcup (a_2\bigsqcup b_2)$

, where

$a_1,a_2\in A,b_1,b_2\in B$

, and

$(a_1\bigsqcup b_1),(a_2\bigsqcup b_2)$

are disjoint. Due to the properties of a disjoint union, the latter condition is equivalent to:

$a_1,a_2$

are disjoint and

$b_1,b_2$

are disjoint.

Each simplex in the right-hand-side complex is of the form $(a_1\bigsqcup a_2)\bigsqcup (b_1\bigsqcup b_2)$, where $a_1,a_2\in A,b_1,b_2\in B$, and $a_1,a_2$ are disjoint and $b_1,b_2$ are disjoint. So the sets of simplices on both sides are exactly the same. □

In particular, the deleted join of the n-dimensional simplex ${\mathrm{\Delta }}^n$ with itself is the n-dimensional crosspolytope, which is homeomorphic to the n-dimensional sphere $S^n$.

Generalization

The n-fold k-wise deleted join of a simplicial complex A is defined as:

$A_{\mathrm{\Delta }(k)}^{*n}:=\{a_1\bigsqcup a_2\bigsqcup \cdots \bigsqcup a_n:a_1,\cdots ,a_n\text{ are k-wise disjoint faces of }A\}$

, where "k-wise disjoint" means that every subset of k have an empty intersection.

In particular, the n-fold n-wise deleted join contains all disjoint unions of n faces whose intersection is empty, and the n-fold 2-wise deleted join is smaller: it contains only the disjoint unions of n faces that are pairwise-disjoint. The 2-fold 2-wise deleted join is just the simple deleted join defined above.

The n-fold 2-wise deleted join of a discrete space with m points is called the (m,n)-chessboard complex.

See also

• Desuspension

References

• Hatcher, Allen, Algebraic topology. Cambridge University Press, Cambridge, 2002. xii+544 pp. ISBN 0-521-79160-X and ISBN 0-521-79540-0
• Brown, Ronald, Topology and Groupoids Section 5.7 Joins.