Hyperbolic equilibrium point

In the study of dynamical systems, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point that does not have any center manifolds. Near a hyperbolic point the orbits of a two-dimensional, non-dissipative system resemble hyperbolas. This fails to hold in general. Strogatz notes that "hyperbolic is an unfortunate name—it sounds like it should mean 'saddle point'—but it has become standard." Several properties hold about a neighborhood of a hyperbolic point, notably

Orbits near a two-dimensional saddle point, an example of a hyperbolic equilibrium.

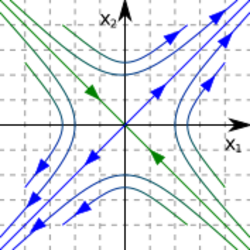
• A stable manifold and an unstable manifold exist,
• Shadowing occurs,
• The dynamics on the invariant set can be represented via symbolic dynamics,
• A natural measure can be defined,
• The system is structurally stable.

Maps

If [math]\displaystyle{ T \colon \mathbb{R}^{n} \to \mathbb{R}^{n} }[/math] is a C¹ map and p is a fixed point then p is said to be a hyperbolic fixed point when the Jacobian matrix [math]\displaystyle{ \operatorname{D} T (p) }[/math] has no eigenvalues with a zero real component.

One example of a map whose only fixed point is hyperbolic is Arnold's cat map:

[math]\displaystyle{ \begin{bmatrix} x_{n+1}\\ y_{n+1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 2\end{bmatrix} \begin{bmatrix} x_n\\ y_n\end{bmatrix} }[/math]

Since the eigenvalues are given by

[math]\displaystyle{ \lambda_1=\frac{3+\sqrt{5}}{2} }[/math]

[math]\displaystyle{ \lambda_2=\frac{3-\sqrt{5}}{2} }[/math]

We know that the Lyapunov exponents are:

[math]\displaystyle{ \lambda_1=\frac{\ln(3+\sqrt{5})}{2}\gt 1 }[/math]

[math]\displaystyle{ \lambda_2=\frac{\ln(3-\sqrt{5})}{2}\lt 1 }[/math]

Therefore it is a saddle point.

Flows

Let [math]\displaystyle{ F \colon \mathbb{R}^{n} \to \mathbb{R}^{n} }[/math] be a C¹ vector field with a critical point p, i.e., F(p) = 0, and let J denote the Jacobian matrix of F at p. If the matrix J has no eigenvalues with zero real parts then p is called hyperbolic. Hyperbolic fixed points may also be called hyperbolic critical points or elementary critical points.

The Hartman–Grobman theorem states that the orbit structure of a dynamical system in a neighbourhood of a hyperbolic equilibrium point is topologically equivalent to the orbit structure of the linearized dynamical system.

Example

Consider the nonlinear system

[math]\displaystyle{ \begin{align} \frac{dx}{dt} & = y, \\[5pt] \frac{dy}{dt} & = -x-x^3-\alpha y,~ \alpha \ne 0 \end{align} }[/math]

(0, 0) is the only equilibrium point. The Jacobian matrix of the linearization at the equilibrium point is

[math]\displaystyle{ J(0,0) = \left[ \begin{array}{rr} 0 & 1 \\ -1 & -\alpha \end{array} \right]. }[/math]

The eigenvalues of this matrix are [math]\displaystyle{ \frac{-\alpha \pm \sqrt{\alpha^2-4}}{2} }[/math]. For all values of α ≠ 0, the eigenvalues have non-zero real part. Thus, this equilibrium point is a hyperbolic equilibrium point. The linearized system will behave similar to the non-linear system near (0, 0). When α = 0, the system has a nonhyperbolic equilibrium at (0, 0).

Comments

In the case of an infinite dimensional system—for example systems involving a time delay—the notion of the "hyperbolic part of the spectrum" refers to the above property.

See also

• Anosov flow
• Hyperbolic set
• Normally hyperbolic invariant manifold