Fixed point (mathematics)

Short description: Element mapped to itself by a mathematical function

Fixed points in mathematics are not to be confused with other uses of "fixed point", or stationary points where f'(x) = 0.

A function with three fixed points

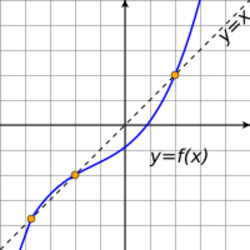
In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation. Specifically, for functions, a fixed point is an element that is mapped to itself by the function.

Fixed point of a function

Formally, c is a fixed point of a function f if c belongs to both the domain and the codomain of f, and f(c) = c.

For example, if f is defined on the real numbers by [math]\displaystyle{ f(x) = x^2 - 3 x + 4, }[/math] then 2 is a fixed point of f, because f(2) = 2.

Not all functions have fixed points: for example, f(x) = x + 1, has no fixed points, since x is never equal to x + 1 for any real number. In graphical terms, a fixed-point x means the point (x, f(x)) is on the line y = x, or in other words the graph of f has a point in common with that line.

Fixed point iteration

In numerical analysis, fixed-point iteration is a method of computing fixed points of a function. Specifically, given a function [math]\displaystyle{ f }[/math] with the same domain and codomain, a point [math]\displaystyle{ x_0 }[/math] in the domain of [math]\displaystyle{ f }[/math], the fixed-point iteration is

[math]\displaystyle{ x_{n+1}=f(x_n), \, n=0, 1, 2, \dots }[/math]

which gives rise to the sequence [math]\displaystyle{ x_0, x_1, x_2, \dots }[/math] of iterated function applications [math]\displaystyle{ x_0, f(x_0), f(f(x_0)), \dots }[/math] which is hoped to converge to a point [math]\displaystyle{ x }[/math]. If [math]\displaystyle{ f }[/math] is continuous, then one can prove that the obtained [math]\displaystyle{ x }[/math] is a fixed point of [math]\displaystyle{ f }[/math].

The notions of attracting fixed points, repelling fixed points, and periodic points are defined with respect to fixed-point iteration.

Fixed-point theorems

A fixed-point theorem is a result saying that at least one fixed point exists, under some general condition.

For example, the Banach fixed-point theorem (1922) gives a general criterion guaranteeing that, if it is satisfied, fixed-point iteration will always converge to a fixed point.

The Brouwer fixed-point theorem (1911) says that any continuous function from the closed unit ball in n-dimensional Euclidean space to itself must have a fixed point, but it doesn't describe how to find the fixed point.

The Lefschetz fixed-point theorem (and the Nielsen fixed-point theorem) from algebraic topology give a way to count fixed points.

Fixed point of a group action

In algebra, for a group G acting on a set X with a group action [math]\displaystyle{ \cdot }[/math], x in X is said to be a fixed point of g if [math]\displaystyle{ g \cdot x = x }[/math].

The fixed-point subgroup [math]\displaystyle{ G^f }[/math] of an automorphism f of a group G is the subgroup of G: [math]\displaystyle{ G^f = \{ g \in G \mid f(g) = g \}. }[/math]

Similarly, the fixed-point subring [math]\displaystyle{ R^f }[/math] of an automorphism f of a ring R is the subring of the fixed points of f, that is, [math]\displaystyle{ R^f = \{ r \in R \mid f(r) = r \}. }[/math]

In Galois theory, the set of the fixed points of a set of field automorphisms is a field called the fixed field of the set of automorphisms.

Topological fixed point property

A topological space [math]\displaystyle{ X }[/math] is said to have the fixed point property (FPP) if for any continuous function

[math]\displaystyle{ f\colon X \to X }[/math]

there exists [math]\displaystyle{ x \in X }[/math] such that [math]\displaystyle{ f(x)=x }[/math].

The FPP is a topological invariant, i.e. is preserved by any homeomorphism. The FPP is also preserved by any retraction.

According to the Brouwer fixed-point theorem, every compact and convex subset of a Euclidean space has the FPP. Compactness alone does not imply the FPP, and convexity is not even a topological property, so it makes sense to ask how to topologically characterize the FPP. In 1932 Borsuk asked whether compactness together with contractibility could be a necessary and sufficient condition for the FPP to hold. The problem was open for 20 years until the conjecture was disproved by Kinoshita who found an example of a compact contractible space without the FPP.

Fixed points of partial orders

In domain theory, the notion and terminology of fixed points is generalized to a partial order. Let ≤ be a partial order over a set X and let f: X → X be a function over X. Then a prefixed point (also spelled pre-fixed point, sometimes shortened to prefixpoint or pre-fixpoint) of f is any p such that f(p) ≤ p. Analogously, a postfixed point of f is any p such that p ≤ f(p). The opposite usage occasionally appears. Malkis justifies the definition presented here as follows: "since f is before the inequality sign in the term f(x) ≤ x, such x is called a prefix point." A fixed point is a point that is both a prefixpoint and a postfixpoint. Prefixpoints and postfixpoints have applications in theoretical computer science.

Least fixed point

In order theory, the least fixed point of a function from a partially ordered set (poset) to itself is the fixed point which is less than each other fixed point, according to the order of the poset. A function need not have a least fixed point, but if it does then the least fixed point is unique.

One way to express the Knaster–Tarski theorem is to say that a monotone function on a complete lattice has a least fixpoint that coincides with its least prefixpoint (and similarly its greatest fixpoint coincides with its greatest postfixpoint).

Fixed-point combinator

In combinatory logic for computer science, a fixed-point combinator is a higher-order function [math]\displaystyle{ \mathsf{fix} }[/math] that returns a fixed point of its argument function, if one exists. Formally, if the function f has one or more fixed points, then

[math]\displaystyle{ \operatorname{\mathsf{fix}}f = f(\operatorname{\mathsf{fix}}f). }[/math]

Fixed-point logics

In mathematical logic, fixed-point logics are extensions of classical predicate logic that have been introduced to express recursion. Their development has been motivated by descriptive complexity theory and their relationship to database query languages, in particular to Datalog.

Applications

In many fields, equilibria or stability are fundamental concepts that can be described in terms of fixed points. Some examples follow.

• In projective geometry, a fixed point of a projectivity has been called a double point.
• In economics, a Nash equilibrium of a game is a fixed point of the game's best response correspondence. John Nash exploited the Kakutani fixed-point theorem for his seminal paper that won him the Nobel prize in economics.
• In physics, more precisely in the theory of phase transitions, linearization near an unstable fixed point has led to Wilson's Nobel prize-winning work inventing the renormalization group, and to the mathematical explanation of the term "critical phenomenon."
• Programming language compilers use fixed point computations for program analysis, for example in data-flow analysis, which is often required for code optimization. They are also the core concept used by the generic program analysis method abstract interpretation.
• In type theory, the fixed-point combinator allows definition of recursive functions in the untyped lambda calculus.
• The vector of PageRank values of all web pages is the fixed point of a linear transformation derived from the World Wide Web's link structure.
• The stationary distribution of a Markov chain is the fixed point of the one step transition probability function.
• Fixed points are used to finding formulas for iterated functions.

See also

• Cycles and fixed points of permutations
• Eigenvector
• Equilibrium
• Fixed points of a Möbius transformation
• Idempotence
• Infinite compositions of analytic functions

• Invariant (mathematics)

External links

• An Elegant Solution for Drawing a Fixed Point