Icosahedral prism
From HandWiki
| Icosahedral prism | |
|---|---|
| Type | Prismatic uniform 4-polytope |
| Uniform index | 59 |
| Schläfli symbol | t{2,3,5} or {3,5}×{} s{3,4}×{} sr{3,3}×{} |
| Coxeter-Dynkin |       
|
| Cells | 2 (3.3.3.3.3) 20 (3.4.4) 
|
| Faces | 30 {4} 40 {3} |
| Edges | 72 |
| Vertices | 24 |
| Vertex figure | 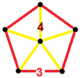 pentagonal pyramids |
| Dual | Dodecahedral bipyramid |
| Symmetry group | [5,3,2], order 240 [3+,4,2], order 48 [(3,3)+,2], order 24 |
| Properties | convex |
In geometry, an icosahedral prism is a convex uniform 4-polytope (four-dimensional polytope). This 4-polytope has 22 polyhedral cells: 2 icosahedra connected by 20 triangular prisms. It has 70 faces: 30 squares and 40 triangles. It has 72 edges and 24 vertices.
It can be constructed by creating two coinciding icosahedra in 3-space, and translating each copy in opposite perpendicular directions in 4-space until their separation equals their edge length.
It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids or Archimedean solids.
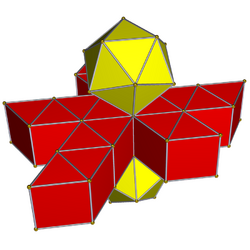 Net |
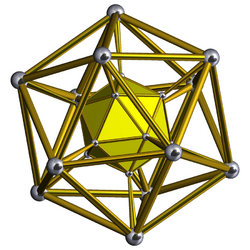 Schlegel diagram Only one icosahedral cell shown |
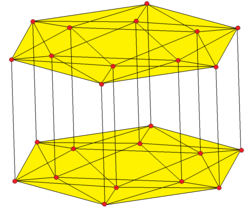 Orthographic projection |
Alternate names
- Icosahedral dyadic prism Norman W. Johnson
- Ipe for icosahedral prism/hyperprism (Jonathan Bowers)
- Snub tetrahedral prism/hyperprism
Related polytopes
- Snub tetrahedral antiprism - [math]\displaystyle{ s\left\{\begin{array}{l}3\\3\\2\end{array}\right\} }[/math] = ht0,1,2,3{3,3,2} or
, a related nonuniform 4-polytope
External links
- 6. Convex uniform prismatic polychora - Model 59, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x o3o5x - ipe". https://bendwavy.org/klitzing/dimensions/polychora.htm.
 |  |
