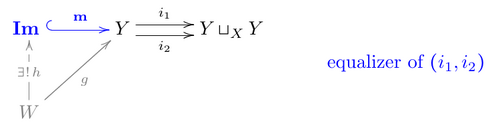Image (category theory)
In category theory, a branch of mathematics, the image of a morphism is a generalization of the image of a function.
General definition
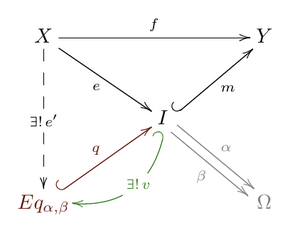
Given a category [math]\displaystyle{ C }[/math] and a morphism [math]\displaystyle{ f\colon X\to Y }[/math] in [math]\displaystyle{ C }[/math], the image[1] of [math]\displaystyle{ f }[/math] is a monomorphism [math]\displaystyle{ m\colon I\to Y }[/math] satisfying the following universal property:
- There exists a morphism [math]\displaystyle{ e\colon X\to I }[/math] such that [math]\displaystyle{ f = m\, e }[/math].
- For any object [math]\displaystyle{ I' }[/math] with a morphism [math]\displaystyle{ e'\colon X\to I' }[/math] and a monomorphism [math]\displaystyle{ m'\colon I'\to Y }[/math] such that [math]\displaystyle{ f = m'\, e' }[/math], there exists a unique morphism [math]\displaystyle{ v\colon I\to I' }[/math] such that [math]\displaystyle{ m = m'\, v }[/math].
Remarks:
- such a factorization does not necessarily exist.
- [math]\displaystyle{ e }[/math] is unique by definition of [math]\displaystyle{ m }[/math] monic.
- [math]\displaystyle{ m'e'=f=me=m've }[/math], therefore [math]\displaystyle{ e'=ve }[/math] by [math]\displaystyle{ m' }[/math] monic.
- [math]\displaystyle{ v }[/math] is monic.
- [math]\displaystyle{ m = m'\, v }[/math] already implies that [math]\displaystyle{ v }[/math] is unique.
The image of [math]\displaystyle{ f }[/math] is often denoted by [math]\displaystyle{ \text{Im} f }[/math] or [math]\displaystyle{ \text{Im} (f) }[/math].
Proposition: If [math]\displaystyle{ C }[/math] has all equalizers then the [math]\displaystyle{ e }[/math] in the factorization [math]\displaystyle{ f= m\, e }[/math] of (1) is an epimorphism.[2]
Let [math]\displaystyle{ \alpha,\, \beta }[/math] be such that [math]\displaystyle{ \alpha\, e =\beta\, e }[/math], one needs to show that [math]\displaystyle{ \alpha=\beta }[/math]. Since the equalizer of [math]\displaystyle{ (\alpha, \beta) }[/math] exists, [math]\displaystyle{ e }[/math] factorizes as [math]\displaystyle{ e= q\, e' }[/math] with [math]\displaystyle{ q }[/math] monic. But then [math]\displaystyle{ f= (m\, q)\, e' }[/math] is a factorization of [math]\displaystyle{ f }[/math] with [math]\displaystyle{ (m\, q) }[/math] monomorphism. Hence by the universal property of the image there exists a unique arrow [math]\displaystyle{ v: I \to Eq_{\alpha,\beta} }[/math] such that [math]\displaystyle{ m = m\,q\, v }[/math] and since [math]\displaystyle{ m }[/math] is monic [math]\displaystyle{ \text{id}_I = q\, v }[/math]. Furthermore, one has [math]\displaystyle{ m\, q = (m q v)\,q }[/math] and by the monomorphism property of [math]\displaystyle{ mq }[/math] one obtains [math]\displaystyle{ \text{id}_{Eq_{\alpha,\beta}}= v\, q }[/math].
This means that [math]\displaystyle{ I \equiv Eq_{\alpha,\beta} }[/math] and thus that [math]\displaystyle{ \text{id}_I = q\, v }[/math] equalizes [math]\displaystyle{ (\alpha, \beta) }[/math], whence [math]\displaystyle{ \alpha = \beta }[/math].
Second definition
In a category [math]\displaystyle{ C }[/math] with all finite limits and colimits, the image is defined as the equalizer [math]\displaystyle{ (Im,m) }[/math] of the so-called cokernel pair [math]\displaystyle{ (Y \sqcup_X Y, i_1, i_2) }[/math], which is the cocartesian of a morphism with itself over its domain, which will result in a pair of morphisms [math]\displaystyle{ i_1,i_2:Y\to Y\sqcup_X Y }[/math], on which the equalizer is taken, i.e. the first of the following diagrams is cocartesian, and the second equalizing.[3]
Remarks:
- Finite bicompleteness of the category ensures that pushouts and equalizers exist.
- [math]\displaystyle{ (Im,m) }[/math] can be called regular image as [math]\displaystyle{ m }[/math] is a regular monomorphism, i.e. the equalizer of a pair of morphisms. (Recall also that an equalizer is automatically a monomorphism).
- In an abelian category, the cokernel pair property can be written [math]\displaystyle{ i_1\, f = i_2\, f\ \Leftrightarrow\ (i_1 - i_2)\, f = 0 = 0\, f }[/math] and the equalizer condition [math]\displaystyle{ i_1\, m = i_2\, m\ \Leftrightarrow\ (i_1 - i_2)\, m = 0 \, m }[/math]. Moreover, all monomorphisms are regular.
Theorem — If [math]\displaystyle{ f }[/math] always factorizes through regular monomorphisms, then the two definitions coincide.
First definition implies the second: Assume that (1) holds with [math]\displaystyle{ m }[/math] regular monomorphism.
- Equalization: one needs to show that [math]\displaystyle{ i_1\, m= i_2\, m }[/math] . As the cokernel pair of [math]\displaystyle{ f,\ i_1\, f= i_2\, f }[/math] and by previous proposition, since [math]\displaystyle{ C }[/math] has all equalizers, the arrow [math]\displaystyle{ e }[/math] in the factorization [math]\displaystyle{ f= m\, e }[/math] is an epimorphism, hence [math]\displaystyle{ i_1\, f= i_2\, f\ \Rightarrow \ i_1\, m= i_2\, m }[/math].
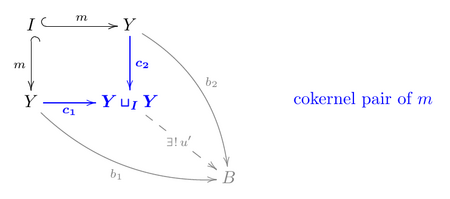
- Universality: in a category with all colimits (or at least all pushouts) [math]\displaystyle{ m }[/math] itself admits a cokernel pair [math]\displaystyle{ (Y \sqcup_{I}Y, c_1, c_2) }[/math]
- Moreover, as a regular monomorphism, [math]\displaystyle{ (I,m) }[/math] is the equalizer of a pair of morphisms [math]\displaystyle{ b_1, b_2: Y \longrightarrow B }[/math] but we claim here that it is also the equalizer of [math]\displaystyle{ c_1, c_2: Y \longrightarrow Y \sqcup_{I}Y }[/math].
- Indeed, by construction [math]\displaystyle{ b_1\, m = b_2\, m }[/math] thus the "cokernel pair" diagram for [math]\displaystyle{ m }[/math] yields a unique morphism [math]\displaystyle{ u': Y \sqcup_{I}Y \longrightarrow B }[/math] such that [math]\displaystyle{ b_1 = u'\, c_1,\ b_2 = u'\, c_2 }[/math]. Now, a map [math]\displaystyle{ m': I'\longrightarrow Y }[/math] which equalizes [math]\displaystyle{ (c_1, c_2) }[/math] also satisfies [math]\displaystyle{ b_1\, m'= u'\, c_1 \, m'= u'\, c_2\, m'= b_2\, m' }[/math], hence by the equalizer diagram for [math]\displaystyle{ (b_1, b_2) }[/math], there exists a unique map [math]\displaystyle{ h': I'\to I }[/math] such that [math]\displaystyle{ m'= m\, h' }[/math].
- Finally, use the cokernel pair diagram (of [math]\displaystyle{ f }[/math]) with [math]\displaystyle{ j_1 := c_1,\ j_2 := c_2,\ Z:= Y\sqcup_I Y }[/math] : there exists a unique [math]\displaystyle{ u: Y \sqcup_{X}Y \longrightarrow Y\sqcup_I Y }[/math] such that [math]\displaystyle{ c_1 = u\, i_1,\ c_2 = u\, i_2 }[/math]. Therefore, any map [math]\displaystyle{ g }[/math] which equalizes [math]\displaystyle{ (i_1, i_2) }[/math] also equalizes [math]\displaystyle{ (c_1, c_2) }[/math] and thus uniquely factorizes as [math]\displaystyle{ g= m\, h' }[/math]. This exactly means that [math]\displaystyle{ (I,m) }[/math] is the equalizer of [math]\displaystyle{ (i_1, i_2) }[/math].
Second definition implies the first:
- Factorization: taking [math]\displaystyle{ m' := f }[/math] in the equalizer diagram ([math]\displaystyle{ m' }[/math] corresponds to [math]\displaystyle{ g }[/math]), one obtains the factorization [math]\displaystyle{ f = m\, h }[/math].
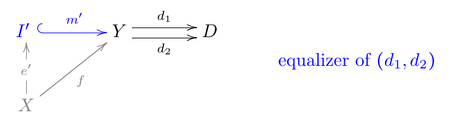
- Universality: let [math]\displaystyle{ f = m'\, e' }[/math] be a factorization with [math]\displaystyle{ m' }[/math] regular monomorphism, i.e. the equalizer of some pair [math]\displaystyle{ (d_1, d_2) }[/math].
- Then [math]\displaystyle{ d_1\, m'= d_2\, m'\ \Rightarrow \ d_1\, f=d_1\, m'\, e= d_2\, m'\, e= d_2\, f }[/math] so that by the "cokernel pair" diagram (of [math]\displaystyle{ f }[/math]), with [math]\displaystyle{ j_1 := d_1,\ j_2 := d_2,\ Z:= D }[/math], there exists a unique [math]\displaystyle{ u'': Y \sqcup_{X}Y \longrightarrow D }[/math] such that [math]\displaystyle{ d_1 = u''\, i_1,\ d_2 = u''\, i_2 }[/math].
- Now, from [math]\displaystyle{ i_1\, m= i_2\, m }[/math] (m from the equalizer of (i1, i2) diagram), one obtains [math]\displaystyle{ d_1\, m= u''\, i_1\, m = u''\, i_2\, m = d_2\, m }[/math], hence by the universality in the (equalizer of (d1, d2) diagram, with f replaced by m), there exists a unique [math]\displaystyle{ v: Im \longrightarrow I' }[/math] such that [math]\displaystyle{ m = m'\, v }[/math].
Examples
In the category of sets the image of a morphism [math]\displaystyle{ f\colon X \to Y }[/math] is the inclusion from the ordinary image [math]\displaystyle{ \{f(x) ~|~ x \in X\} }[/math] to [math]\displaystyle{ Y }[/math]. In many concrete categories such as groups, abelian groups and (left- or right) modules, the image of a morphism is the image of the correspondent morphism in the category of sets.
In any normal category with a zero object and kernels and cokernels for every morphism, the image of a morphism [math]\displaystyle{ f }[/math] can be expressed as follows:
- im f = ker coker f
In an abelian category (which is in particular binormal), if f is a monomorphism then f = ker coker f, and so f = im f.
See also
References
- ↑ Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics, 17, Academic Press, ISBN 978-0-12-499250-4 Section I.10 p.12
- ↑ Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics, 17, Academic Press, ISBN 978-0-12-499250-4 Proposition 10.1 p.12
- ↑ Kashiwara, Masaki; Schapira, Pierre (2006), "Categories and Sheaves", Grundlehren der Mathematischen Wissenschaften, 332, Berlin Heidelberg: Springer, pp. 113–114 Definition 5.1.1
 |