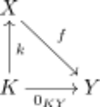Kernel (category theory)

Short description: Generalization of the kernel of a homomorphism

In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra. Intuitively, the kernel of the morphism f : X → Y is the "most general" morphism k : K → X that yields zero when composed with (followed by) f.

Note that kernel pairs and difference kernels (also known as binary equalisers) sometimes go by the name "kernel"; while related, these aren't quite the same thing and are not discussed in this article.

Definition

Let C be a category. In order to define a kernel in the general category-theoretical sense, C needs to have zero morphisms. In that case, if f : X → Y is an arbitrary morphism in C, then a kernel of f is an equaliser of f and the zero morphism from X to Y. In symbols:

ker(f) = eq(f, 0_XY)

To be more explicit, the following universal property can be used. A kernel of f is an object K together with a morphism k : K → X such that:

• f ∘k is the zero morphism from K to Y;

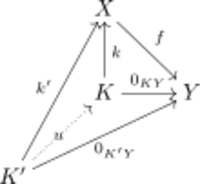
• Given any morphism k′ : K′ → X such that f ∘k′ is the zero morphism, there is a unique morphism u : K′ → K such that k∘u = k′.

As for every universal property, there is a unique isomorphism between two kernels of the same morphism, and the morphism k is always a monomorphism (in the categorical sense). So, it is common to talk of the kernel of a morphism. In concrete categories, one can thus take a subset of K′ for K, in which case, the morphism k is the inclusion map. This allows one to talk of K as the kernel, since f is implicitly defined by K. There are non-concrete categories, where one can similarly define a "natural" kernel, such that K defines k implicitly.

Not every morphism needs to have a kernel, but if it does, then all its kernels are isomorphic in a strong sense: if k : K → X and ℓ : L → X are kernels of f : X → Y, then there exists a unique isomorphism φ : K → L such that ℓ∘φ = k.

Examples

Kernels are familiar in many categories from abstract algebra, such as the category of groups or the category of (left) modules over a fixed ring (including vector spaces over a fixed field). To be explicit, if f : X → Y is a homomorphism in one of these categories, and K is its kernel in the usual algebraic sense, then K is a subalgebra of X and the inclusion homomorphism from K to X is a kernel in the categorical sense.

Note that in the category of monoids, category-theoretic kernels exist just as for groups, but these kernels don't carry sufficient information for algebraic purposes. Therefore, the notion of kernel studied in monoid theory is slightly different (see #Relationship to algebraic kernels below).

In the category of unital rings, there are no kernels in the category-theoretic sense; indeed, this category does not even have zero morphisms. Nevertheless, there is still a notion of kernel studied in ring theory that corresponds to kernels in the category of non-unital rings.

In the category of pointed topological spaces, if f : X → Y is a continuous pointed map, then the preimage of the distinguished point, K, is a subspace of X. The inclusion map of K into X is the categorical kernel of f.

Relation to other categorical concepts

The dual concept to that of kernel is that of cokernel. That is, the kernel of a morphism is its cokernel in the opposite category, and vice versa.

As mentioned above, a kernel is a type of binary equaliser, or difference kernel. Conversely, in a preadditive category, every binary equaliser can be constructed as a kernel. To be specific, the equaliser of the morphisms f and g is the kernel of the difference g − f. In symbols:

eq (f, g) = ker (g − f).

It is because of this fact that binary equalisers are called "difference kernels", even in non-preadditive categories where morphisms cannot be subtracted.

Every kernel, like any other equaliser, is a monomorphism. Conversely, a monomorphism is called normal if it is the kernel of some morphism. A category is called normal if every monomorphism is normal.

Abelian categories, in particular, are always normal. In this situation, the kernel of the cokernel of any morphism (which always exists in an abelian category) turns out to be the image of that morphism; in symbols:

im f = ker coker f (in an abelian category)

When m is a monomorphism, it must be its own image; thus, not only are abelian categories normal, so that every monomorphism is a kernel, but we also know which morphism the monomorphism is a kernel of, to wit, its cokernel. In symbols:

m = ker (coker m) (for monomorphisms in an abelian category)

Relationship to algebraic kernels

Universal algebra defines a notion of kernel for homomorphisms between two algebraic structures of the same kind. This concept of kernel measures how far the given homomorphism is from being injective. There is some overlap between this algebraic notion and the categorical notion of kernel since both generalize the situation of groups and modules mentioned above. In general, however, the universal-algebraic notion of kernel is more like the category-theoretic concept of kernel pair. In particular, kernel pairs can be used to interpret kernels in monoid theory or ring theory in category-theoretic terms.

Sources

• Awodey, Steve (2010). Category Theory. Oxford Logic Guides. 49 (2nd ed.). Oxford University Press. ISBN 978-0-19-923718-0. http://angg.twu.net/MINICATS/awodey__category_theory.pdf. Retrieved 2018-06-29. 
• Kernel in nLab