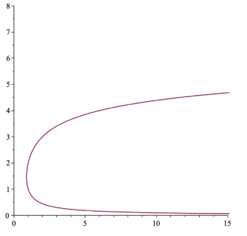
Inverse gamma function

Short description: Inverse of the gamma function

Graph of an inverse gamma function

Plot of inverse gamma function in the complex plane

In mathematics, the inverse gamma function [math]\displaystyle{ \Gamma^{-1}(x) }[/math] is the inverse function of the gamma function. In other words, [math]\displaystyle{ y = \Gamma^{-1}(x) }[/math] whenever [math]\displaystyle{ \Gamma(y)=x }[/math]. For example, [math]\displaystyle{ \Gamma^{-1}(24)=5 }[/math]. Usually, the inverse gamma function refers to the principal branch with domain on the real interval [math]\displaystyle{ \left[\beta, +\infty\right) }[/math] and image on the real interval [math]\displaystyle{ \left[\alpha, +\infty\right) }[/math], where [math]\displaystyle{ \beta = 0.8856031\ldots }[/math] is the minimum value of the gamma function on the positive real axis and [math]\displaystyle{ \alpha = \Gamma^{-1}(\beta) = 1.4616321\ldots }[/math] is the location of that minimum.

Definition

The inverse gamma function may be defined by the following integral representation [math]\displaystyle{ \Gamma^{-1}(x)=a+bx+\int_{-\infty}^{\Gamma(\alpha)}\left(\frac{1}{x-t}-\frac{t}{t^{2}-1}\right)d\mu(t)\,, }[/math] where [math]\displaystyle{ \mu (t) }[/math] is a Borel measure such that [math]\displaystyle{ \int_{-\infty}^{\Gamma\left(\alpha\right)}\left(\frac{1}{t^{2}+1}\right)d\mu(t)\lt \infty \,, }[/math] and [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are real numbers with [math]\displaystyle{ b \geqq 0 }[/math].

Approximation

To compute the branches of the inverse gamma function one can first compute the Taylor series of [math]\displaystyle{ \Gamma(x) }[/math] near [math]\displaystyle{ \alpha }[/math]. The series can then be truncated and inverted, which yields successively better approximations to [math]\displaystyle{ \Gamma^{-1}(x) }[/math]. For instance, we have the quadratic approximation:

[math]\displaystyle{ \Gamma^{-1}\left(x\right)\approx\alpha+\sqrt{\frac{2\left(x-\Gamma\left(\alpha\right)\right)}{\Psi\left(1,\ \alpha\right)\Gamma\left(\alpha\right)}}. }[/math]

The inverse gamma function also has the following asymptotic formula [math]\displaystyle{ \Gamma^{-1}(x)\sim\frac{1}{2}+\frac{\ln\left(\frac{x}{\sqrt{2\pi}}\right)}{W_{0}\left(e^{-1}\ln\left(\frac{x}{\sqrt{2\pi}}\right)\right)}\,, }[/math] where [math]\displaystyle{ W_0(x) }[/math] is the Lambert W function. The formula is found by inverting the Stirling approximation, and so can also be expanded into an asymptotic series.

Series expansion

To obtain a series expansion of the inverse gamma function one can first compute the series expansion of the reciprocal gamma function [math]\displaystyle{ \frac{1}{\Gamma(x)} }[/math] near the poles at the negative integers, and then invert the series.

Setting [math]\displaystyle{ z=\frac{1}{x} }[/math] then yields, for the n th branch [math]\displaystyle{ \Gamma_{n}^{-1}(z) }[/math] of the inverse gamma function ([math]\displaystyle{ n\ge 0 }[/math]) [math]\displaystyle{ \Gamma_{n}^{-1}(z)=-n+\frac{\left(-1\right)^{n}}{n!z}+\frac{\psi^{(0)}\left(n+1\right)}{\left(n!z\right)^2}+\frac{\left(-1\right)^{n}\left(\pi^{2}+9\psi^{(0)}\left(n+1\right)^{2}-3\psi^{(1)}\left(n+1\right)\right)}{6\left(n!z\right)^3}+O\left(\frac{1}{z^{4}}\right)\,, }[/math] where [math]\displaystyle{ \psi^{(n)}(x) }[/math] is the polygamma function.