Isotomic conjugate

Short description: Point constructed from another point and a reference triangle

In geometry, the isotomic conjugate of a point P with respect to a triangle △ABC is another point, defined in a specific way from P and △ABC: If the base points of the lines PA, PB, PC on the sides opposite A, B, C are reflected about the midpoints of their respective sides, the resulting lines intersect at the isotomic conjugate of P.

Construction

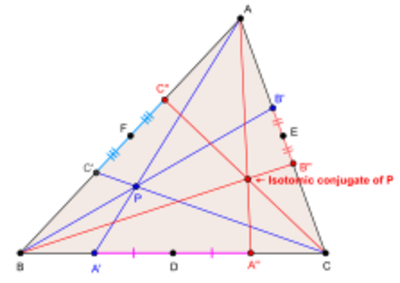
We assume that P is not collinear with any two vertices of △ABC. Let A', B', C' be the points in which the lines AP, BP, CP meet sidelines BC, CA, AB (extended if necessary). Reflecting A', B', C' in the midpoints of sides BC, CA, AB will give points A", B", C" respectively. The isotomic lines AA", BB", CC" joining these new points to the vertices meet at a point (which can be proved using Ceva's theorem), the isotomic conjugate of P.

If the trilinears for P are p : q : r, then the trilinears for the isotomic conjugate of P are

[math]\displaystyle{ a^{-2}p^{-1} : b^{-2}q^{-1} : c^{-2}r^{-1}, }[/math]

where a, b, c are the side lengths opposite vertices A, B, C respectively.

Properties

The isotomic conjugate of the centroid of triangle △ABC is the centroid itself.

The isotomic conjugate of the symmedian point is the third Brocard point, and the isotomic conjugate of the Gergonne point is the Nagel point.

Isotomic conjugates of lines are circumconics, and conversely, isotomic conjugates of circumconics are lines. (This property holds for isogonal conjugates as well.)

See also

• Isogonal conjugate
• Triangle center

References

• Robert Lachlan, An Elementary Treatise on Modern Pure Geometry, Macmillan and Co., 1893, page 57.
• Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN:978-0-486-46237-0, pp. 157–159, 278

External links

• Weisstein, Eric W.. "Isotomic Conjugate". http://mathworld.wolfram.com/IsotomicConjugate.html. 
• Pauk Yiu: Isotomic and isogonal conjugates
• Navneel Singhal: Isotomic and isogonal conjugates

zh:等角共轭