k-cell (mathematics)

Short description: Higher-dimensional version of a rectangle or rectangular solid

Projections of K-cells onto the plane (from [math]\displaystyle{ k=1 }[/math] to [math]\displaystyle{ 6 }[/math]). Only the edges of the higher-dimensional cells are shown.

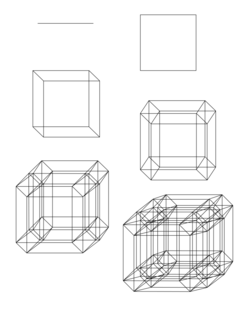
A [math]\displaystyle{ k }[/math]-cell is a higher-dimensional version of a rectangle or rectangular solid. It is the Cartesian product of [math]\displaystyle{ k }[/math] closed intervals on the real line. This means that a [math]\displaystyle{ k }[/math]-dimensional rectangular solid has each of its edges equal to one of the closed intervals used in the definition. The [math]\displaystyle{ k }[/math] intervals need not be identical. For example, a 2-cell is a rectangle in [math]\displaystyle{ \mathbb{R}^2 }[/math] such that the sides of the rectangles are parallel to the coordinate axes. Every [math]\displaystyle{ k }[/math]-cell is compact.

Formal definition

For every integer [math]\displaystyle{ i }[/math] from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ k }[/math], let [math]\displaystyle{ a_i }[/math] and [math]\displaystyle{ b_i }[/math] be real numbers such that for all [math]\displaystyle{ a_i \lt b_i }[/math]. The set of all points [math]\displaystyle{ x=(x_1,\dots,x_k) }[/math] in [math]\displaystyle{ \mathbb{R}^k }[/math] whose coordinates satisfy the inequalities [math]\displaystyle{ a_i\leq x_i\leq b_i }[/math] is a [math]\displaystyle{ k }[/math]-cell.

Intuition

A [math]\displaystyle{ k }[/math]-cell of dimension [math]\displaystyle{ k\leq 3 }[/math] is especially simple. For example, a 1-cell is simply the interval [math]\displaystyle{ [a,b] }[/math] with [math]\displaystyle{ a \lt b }[/math]. A 2-cell is the rectangle formed by the Cartesian product of two closed intervals, and a 3-cell is a rectangular solid.

The sides and edges of a [math]\displaystyle{ k }[/math]-cell need not be equal in (Euclidean) length; although the unit cube (which has boundaries of equal Euclidean length) is a 3-cell, the set of all 3-cells with equal-length edges is a strict subset of the set of all 3-cells.

References

• Foran, James (1991-01-07). Fundamentals of Real Analysis. CRC Press. ISBN 9780824784539. https://books.google.com/books?id=sDjz8x0hJ44C&pg=PA24. Retrieved 23 May 2014. 
• Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill.