Kinetic convex hull

A kinetic convex hull data structure is a kinetic data structure that maintains the convex hull of a set of continuously moving points. It should be distinguished from dynamic convex hull data structures, which handle points undergoing discrete changes such as insertions or deletions of points rather than continuous motion.

The 2D case

The best known data structure for the 2-dimensional kinetic convex hull problem is by Basch, Guibas, and Hershberger. This data structure is responsive, efficient, compact and local.

The data structure

The dual of a convex hull of a set of points is the upper and lower envelopes of the dual set of lines. Therefore, maintaining the upper and lower envelopes of a set of moving lines is equivalent to maintaining the convex hull of a set of moving points. Computing upper and lower envelopes are equivalent problems, so computing the upper envelope of a set of lines is equivalent to computing the convex hull of a set of moving points. The upper envelope of a set of static lines can be computed using a divide and conquer algorithm which partitions the lines into two sets of equal size, calls itself recursively on the two sets to find their upper envelopes, and then merges the two resulting upper envelopes. The merge step is performed using a vertical line sweep. Call the first set of points blue and the second set of points red.

The standard line sweep algorithm for merging upper envelopes sweeps though all of vertices of the red and blue upper envelopes, from left to right. The most recently encountered red and blue points are maintained as the line sweeps. When a point is encountered, the algorithm checks if the point is above or below the segment following the last encountered point of the opposite color. If it is above, that point is added to the merged upper envelope. If it is of a different color than the last added point, the red and blue envelopes have crossed, so the intersection point is also added to the merged upper envelope.

The sequence of edges and vertices resulting from this algorithm is only dependent on the ordering of points, and the results of the line-point comparisons. Thus, the result can be certified with the following certificates:

• x-certificates ([math]\displaystyle{ \lt _x }[/math]) are used to certify the order the vertices of the red and blue envelopes. They are the certificates for a kinetic sorted list on the set of vertices. Since each point involves 2 lines, and the certificate involves 2 points, each certificate involves 4 lines.
• y-certificates ([math]\displaystyle{ \lt _y }[/math]) are used to certify that a vertex is above or below an edge. The certificates appear for all comparisons that would occur during the algorithm.

As long as all of these certificates hold, the merge steps will be executed identically, so the resulting upper envelope will be the same. A kinetic data structure for upper envelopes can be created by using these certificates to certify the static upper envelope algorithm. However, this scheme is not local, because one line many be involved in many y-certificates if it remains on top or bottom as many points from the other envelope are encountered.

Thus, it is necessary to introduce a s-certificates ([math]\displaystyle{ \lt _s }[/math]) which certifies that the slope of a line is greater than or less than the slope of another line.

Having the following certificates for all points ab is sufficient to certify the sequence of edges and vertices resulting from a merge, with only O(1) certificates per line:

The certificates certify structure of the intersection of the red and blue envelopes by certifying intersections(top left) or the absence of intersections(top right and bottom). The arrows indicate which elements are being compared by the certificate.

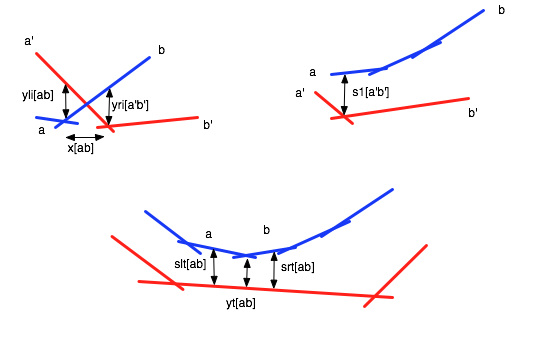
1. [math]\displaystyle{ x[ab] }[/math]: [math]\displaystyle{ ab\lt _x ab.next }[/math]. [math]\displaystyle{ ab.next }[/math] denotes vertex closest to [math]\displaystyle{ ab }[/math] on its right. This certificate is stored for all points [math]\displaystyle{ ab }[/math] which have a different color than the point, [math]\displaystyle{ ab.next }[/math], which follows them.
2. [math]\displaystyle{ yli[ab] }[/math]: [math]\displaystyle{ ab\lt _y ce(ab) }[/math] or [math]\displaystyle{ ab\gt _y ce(ab) }[/math]. This certificate is stored for all points [math]\displaystyle{ ab }[/math] such that [math]\displaystyle{ b }[/math] intersects [math]\displaystyle{ ce(ab) }[/math]. [math]\displaystyle{ ce(ab) }[/math] denotes the contender edge of [math]\displaystyle{ ab }[/math], the edge from the other envelope that is above or below [math]\displaystyle{ ab }[/math].
3. [math]\displaystyle{ yri[ab] }[/math]: [math]\displaystyle{ ab\lt _y ce(ab) }[/math] or [math]\displaystyle{ ab\gt _y ce(ab) }[/math]. This certificate is stored for all points [math]\displaystyle{ ab }[/math] such that [math]\displaystyle{ a }[/math] intersects [math]\displaystyle{ ce(ab) }[/math].
4. [math]\displaystyle{ yt[ab] }[/math]: [math]\displaystyle{ ce(ab)\lt _yab }[/math]. This certificate is stored for all points [math]\displaystyle{ ab }[/math] for which [math]\displaystyle{ a\lt _sce(ab)\lt _s b }[/math] and [math]\displaystyle{ ce(ab)\lt _yab }[/math].
5. [math]\displaystyle{ srt[ab] }[/math]: [math]\displaystyle{ a\lt _sce(ab) }[/math]. This certificate is stored for all points [math]\displaystyle{ ab }[/math] for which [math]\displaystyle{ a\lt _sce(ab)\lt _s b }[/math] and [math]\displaystyle{ ce(ab)\lt _yab }[/math].
6. [math]\displaystyle{ srt[ab] }[/math]: [math]\displaystyle{ ce(ab)\lt _s b }[/math]. This certificate is stored for all points [math]\displaystyle{ ab }[/math] for which [math]\displaystyle{ a\lt _sce(ab)\lt _s b }[/math] and [math]\displaystyle{ ce(ab)\lt _yab }[/math].
7. [math]\displaystyle{ sl[ab] }[/math]: [math]\displaystyle{ b\lt _sce(ab) }[/math]. This certificate is stored for all points [math]\displaystyle{ ab }[/math] for which [math]\displaystyle{ b\lt _sce(ab) }[/math] and [math]\displaystyle{ ab\lt _yce(ab) }[/math].
8. [math]\displaystyle{ sr[ab] }[/math]: [math]\displaystyle{ ce(ab)\lt _sa }[/math]. This certificate is stored for all points [math]\displaystyle{ ab }[/math] for which [math]\displaystyle{ ce(ab)\lt _sa }[/math] and [math]\displaystyle{ ab\lt _yce(ab) }[/math].

The first certificate, [math]\displaystyle{ x[ab] }[/math], certifies the x-ordering of the points in the red and blue envelopes. The second and third certificates, [math]\displaystyle{ yli[ab] }[/math] and [math]\displaystyle{ yri[ab] }[/math], certify intersections of the red and blue envelopes. The remaining 5 certificates, [math]\displaystyle{ yt[ab] }[/math], [math]\displaystyle{ srt[ab] }[/math], [math]\displaystyle{ srt[ab] }[/math], [math]\displaystyle{ sl[ab] }[/math], and [math]\displaystyle{ sr[ab] }[/math] place edges that are not in the upper envelopes in the sequence of slopes of the edges that are above it. If the slope is at the start or end of the sequence, [math]\displaystyle{ sl }[/math] or [math]\displaystyle{ sr }[/math] certify this. If it is in the middle of the sequence [math]\displaystyle{ slt }[/math], and [math]\displaystyle{ srt }[/math] certify this, and [math]\displaystyle{ yt }[/math] certifies that the intersection point of the two lines that the edge's slope is in between, is above it. These one or three certificates suffice to prove that all of the edges are above this line. Unlike the previous scheme all lines are only involved in a constant number of certificates. Whenever of these certificates fail, the merged envelope and certificates can be updated in O(1) time.

The kinetic data structure for convex hull is constructed by using these certificates to certify the recursive merge of the upper envelopes. Whenever certificates fail, their merge is updated, and if the envelope resulting from the merge changes, the changes are propagated up through all merges that depend on the result of the merge.

Performance

This data structure is responsive, local, compact, and efficient. This is due to the logarithmic depth of the merges used to certify the upper envelope.

• Responsive: When a certificate fails, it takes O(1) to fix the merge it certifies. If the resulting envelope changes, the change must be propagated up to all merges that depend on the result of the changed merge. There are O(log n) such mergers, so the update can be performed in O(log n) time total.
• Local: Each line is involved in a most O(log n) certificates. This is because each line is involved in a constant number of certificates in each merge, and each line is in O(log n) merges total.
• Compactness: The maximum number of certificates used in this data structure is O(n log n). This is because each merge involves a number of certificates linear to the number of lines merged. Certifying an upper envelope of n lines requires certificates for the merge upper envelope of the two subsets of n/2 lines, and certificates for the merge of the envelopes. Thus the number of certificates, C(n), required to certify the upper envelope of n lines satisfies the recurrence C(n)=2C(n/2)+O(n), with C(1)=O(1). By the master theorem for divide-and-conquer recurrences, C(n)=O(n log n).
• Efficiency: The maximum number of events processed by this algorithm on algebraic or pseudo-algebraic trajectories is near quadratic, [math]\displaystyle{ O(n^{2+\epsilon}) }[/math] for all [math]\displaystyle{ \epsilon\gt 0 }[/math]. Convex hulls of linearly moving points can change [math]\displaystyle{ \Omega(n^2) }[/math] times. Thus this data structure is efficient.

Higher dimensions

Finding an efficient kinetic data structure for maintaining the convex hull of moving points in dimensions higher than 2 is an open problem.

Related Problems

Kinetic convex hull can be used to solve the following related problems:

• Kinetic diameter
• Kinetic width
• Kinetic minimum box
• Kinetic smallest enclosing disk