Koorde
In peer-to-peer networks, Koorde is a distributed hash table (DHT) system based on the Chord DHT and the De Bruijn graph (De Bruijn sequence). Inheriting the simplicity of Chord, Koorde meets O(log n) hops per node (where n is the number of nodes in the DHT), and hops per lookup request with O(log n) neighbors per node.
The Chord concept is based on a wide range of identifiers (e.g. 2160) in a structure of a ring where an identifier can stand for both node and data. Node-successor is responsible for the whole range of IDs between itself and its predecessor.
De Bruijn's graphs

Koorde is based on Chord but also on the De Bruijn graph (De Bruijn sequence). In a d-dimensional de Bruijn graph, there are 2d nodes, each of which has a unique ID with d bits. The node with ID i is connected to nodes 2i mod 2d and 2i + 1 mod 2d. Thanks to this property, the routing algorithm can route to any destination in d hops by successively "shifting in" the bits of the destination ID but only if the dimensions of the distance between mod 1d and 3d are equal.
Routing a message from node m to node k is accomplished by taking the number m and shifting in the bits of k one at a time until the number has been replaced by k. Each shift corresponds to a routing hop to the next intermediate address; the hop is valid because each node's neighbors are the two possible outcomes of shifting a 0 or 1 onto its own address. Because of the structure of de Bruijn graphs, when the last bit of k has been shifted, the query will be at node k. Node k responds whether key k exists.
Routing example
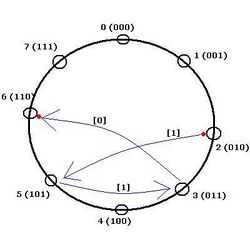
For example, when a message needs to be routed from node 2 (which is 010) to 6 (which is 110), the steps are following:
- Node 2 routes the message to Node 5 (using its connection to 2i + 1 mod 8), shifts the bits left and puts
1as the youngest bit (right side). - Node 5 routes the message to Node 3 (using its connection to 2i + 1 mod 8), shifts the bits left and puts
1as the youngest bit (right side). - Node 3 routes the message to Node 6 (using its connection to 2i mod 8), shifts the bits left and puts
0as the youngest bit (right side).
Non-constant degree Koorde
The d-dimensional de Bruijn can be generalized to base k, in which case node i is connected to nodes k • i + j mod kd, 0 ≤ j < k. The diameter is reduced to Θ(logk n). Koorde node i maintains pointers to k consecutive nodes beginning at the predecessor of k • i mod kd. Each de Bruijn routing step can be emulated with an expected constant number of messages, so routing uses O(logk n) expected hops- For k = Θ(log n), we get Θ(log n) degree and diameter.
Lookup algorithm
function n.lookup(k, shift, i)
{
if k ∈ (n, s]
return (s);
else if i ∈ (n, s]
return p.lookup(k, shift << 1, i ∘ topBit(shift));
else
return s.lookup(k, shift, i);
}
Pseudocode for the Koorde lookup algorithm at node n:
kis the keyIis the imaginary De Bruijn nodepis the reference to the predecessor of2nsis the reference to the successor ofn
References
- "Internet Algorithms" by Greg Plaxton, Fall 2003: [1]
- "Koorde: A simple degree-optimal distributed hash table" by M. Frans Kaashoek and David R. Karger: [2]
- Chord and Koorde descriptions: [3]
 |
