Labelled enumeration theorem

Short description: Counterpart of the Pólya enumeration theorem for the labelled case

In combinatorial mathematics, the labelled enumeration theorem is the counterpart of the Pólya enumeration theorem for the labelled case, where we have a set of labelled objects given by an exponential generating function (EGF) g(z) which are being distributed into n slots and a permutation group G which permutes the slots, thus creating equivalence classes of configurations. There is a special re-labelling operation that re-labels the objects in the slots, assigning labels from 1 to k, where k is the total number of nodes, i.e. the sum of the number of nodes of the individual objects. The EGF [math]\displaystyle{ f_n(z) }[/math] of the number of different configurations under this re-labelling process is given by

[math]\displaystyle{ f_n(z) = \frac{g(z)^n}{|G|}. }[/math]

In particular, if G is the symmetric group of order n (hence, |G| = n!), the functions [math]\displaystyle{ f_n(z) }[/math] can be further combined into a single generating function:

[math]\displaystyle{ F(z,t) = \sum_{n=0}^\infty f_n(z) t^n = \sum_{n=0}^\infty \frac{g(z)^n}{n!} t^n = e^{g(z)t} }[/math]

which is exponential w.r.t. the variable z and ordinary w.r.t. the variable t.

The re-labelling process

A set of cycles being re-labelled to form a permutation. (There are three slots and [math]\displaystyle{ G=S_3 }[/math].)

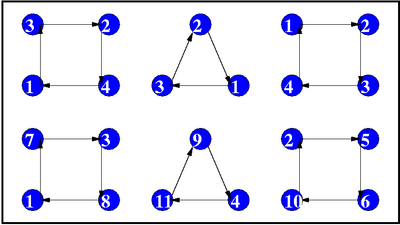
We assume that an object [math]\displaystyle{ \omega }[/math] of size [math]\displaystyle{ |\omega| }[/math] represented by [math]\displaystyle{ z^{|\omega|}/|\omega|! }[/math] contains [math]\displaystyle{ |\omega|=m }[/math] labelled internal nodes, with the labels going from 1 to m. The action of G on the slots is greatly simplified compared to the unlabelled case, because the labels distinguish the objects in the slots, and the orbits under G all have the same size [math]\displaystyle{ |G| }[/math]. (The EGF g(z) may not include objects of size zero. This is because they are not distinguished by labels and therefore the presence of two or more of such objects creates orbits whose size is less than [math]\displaystyle{ |G| }[/math].) As mentioned, the nodes of the objects are re-labelled when they are distributed into the slots. Say an object of size [math]\displaystyle{ r_1 }[/math] goes into the first slot, an object of size [math]\displaystyle{ r_2 }[/math] into the second slot, and so on, and the total size of the configuration is k, so that

[math]\displaystyle{ r_1 + r_2 + \cdots + r_n = k. }[/math]

The re-labelling process works as follows: choose one of

[math]\displaystyle{ {k \choose r_1, r_2, \ldots, r_n} }[/math]

partitions of the set of k labels into subsets of size [math]\displaystyle{ r_1, r_2, \ldots r_n. }[/math] Now re-label the internal nodes of each object using the labels from the respective subset, preserving the order of the labels. E.g. if the first object contains four nodes labelled from 1 to 4 and the set of labels chosen for this object is {2, 5, 6, 10}, then node 1 receives the label 2, node 2, the label 5, node 3, the label 6 and node 4, the label 10. In this way the labels on the objects induce a unique labelling using the labels from the subset of [math]\displaystyle{ [k] }[/math] chosen for the object.

Proof of the theorem

It follows from the re-labelling construction that there are

[math]\displaystyle{ \frac{1}{|G|} \sum_{r_1 + r_2 + \cdots + r_n = k} {k \choose r_1, r_2, \ldots, r_n} \; r_1! [z^{r_1}] g(z) \; r_2! [z^{r_2}] g(z) \; \cdots \; r_n! [z^{r_n}] g(z) }[/math]

or

[math]\displaystyle{ \frac{k!}{|G|} \sum_{r_1 + r_2 + \cdots + r_n = k} [z^{r_1}] g(z) [z^{r_2}] g(z) \cdots [z^{r_n}] g(z) \; = \; \frac{k!}{|G|} [z^k] g(z)^n }[/math]

different configurations of total size k. The formula evaluates to an integer because [math]\displaystyle{ [z^k] g(z)^n }[/math] is zero for k < n (remember that g does not include objects of size zero) and when [math]\displaystyle{ k \ge n }[/math] we have [math]\displaystyle{ n!|k! }[/math] and the order [math]\displaystyle{ |G| }[/math] of G divides the order of [math]\displaystyle{ S_n }[/math], which is [math]\displaystyle{ n! }[/math], by Lagrange's theorem. The conclusion is that the EGF of the labelled configurations is given by

[math]\displaystyle{ f_n(z) = \sum_{k \ge 0} \left( \frac{k!}{|G|} [z^k] g(z)^n \right) \frac{z^k}{k!} = \frac{1}{|G|} \sum_{k \ge 0} z^k [z^k] g(z)^n = \frac{g(z)^n}{|G|}. }[/math]

This formula could also be obtained by enumerating sequences, i.e. the case when the slots are not being permuted, and by using the above argument without the [math]\displaystyle{ 1/|G| }[/math]-factor to show that their generating function under re-labelling is given by [math]\displaystyle{ g(z)^n }[/math]. Finally note that every sequence belongs to an orbit of size [math]\displaystyle{ |G| }[/math], hence the generating function of the orbits is given by [math]\displaystyle{ g(z)^n/|G|. }[/math]

References

• François Bergeron, Gilbert Labelle, Pierre Leroux, Théorie des espèces et combinatoire des structures arborescentes, LaCIM, Montréal (1994). English version: Combinatorial Species and Tree-like Structures, Cambridge University Press (1998).