Legendre rational functions

Short description: Sequence of orthogonal functions on [0, ∞)

Plot of the Legendre rational functions for n=0,1,2 and 3 for x between 0.01 and 100.

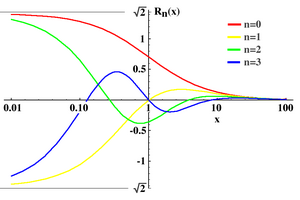
In mathematics, the Legendre rational functions are a sequence of orthogonal functions on [0, ∞). They are obtained by composing the Cayley transform with Legendre polynomials.

A rational Legendre function of degree n is defined as:

[math]\displaystyle{ R_n(x) = \frac{\sqrt{2}}{x+1}\,P_n\left(\frac{x-1}{x+1}\right) }[/math]

where [math]\displaystyle{ P_n(x) }[/math] is a Legendre polynomial. These functions are eigenfunctions of the singular Sturm–Liouville problem:

[math]\displaystyle{ (x+1)\partial_x(x\partial_x((x+1)v(x)))+\lambda v(x)=0 }[/math]

with eigenvalues

[math]\displaystyle{ \lambda_n=n(n+1)\, }[/math]

Properties

Many properties can be derived from the properties of the Legendre polynomials of the first kind. Other properties are unique to the functions themselves.

Recursion

[math]\displaystyle{ R_{n+1}(x)=\frac{2n+1}{n+1}\,\frac{x-1}{x+1}\,R_n(x)-\frac{n}{n+1}\,R_{n-1}(x)\quad\mathrm{for\,n\ge 1} }[/math]

and

[math]\displaystyle{ 2(2n+1)R_n(x)=(x+1)^2(\partial_x R_{n+1}(x)-\partial_x R_{n-1}(x))+(x+1)(R_{n+1}(x)-R_{n-1}(x)) }[/math]

Limiting behavior

Plot of the seventh order (n=7) Legendre rational function multiplied by 1+x for x between 0.01 and 100. Note that there are n zeroes arranged symmetrically about x=1 and if x₀ is a zero, then 1/x₀ is a zero as well. These properties hold for all orders.

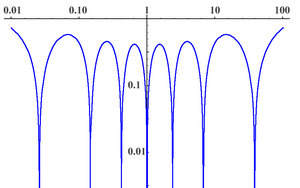
It can be shown that

[math]\displaystyle{ \lim_{x\rightarrow \infty}(x+1)R_n(x)=\sqrt{2} }[/math]

and

[math]\displaystyle{ \lim_{x\rightarrow \infty}x\partial_x((x+1)R_n(x))=0 }[/math]

Orthogonality

[math]\displaystyle{ \int_{0}^\infty R_m(x)\,R_n(x)\,dx=\frac{2}{2n+1}\delta_{nm} }[/math]

where [math]\displaystyle{ \delta_{nm} }[/math] is the Kronecker delta function.

Particular values

[math]\displaystyle{ R_0(x)=\frac{\sqrt{2}}{x+1}\,1\, }[/math]

[math]\displaystyle{ R_1(x)=\frac{\sqrt{2}}{x+1}\,\frac{x-1}{x+1}\, }[/math]

[math]\displaystyle{ R_2(x)=\frac{\sqrt{2}}{x+1}\,\frac{x^2-4x+1}{(x+1)^2}\, }[/math]

[math]\displaystyle{ R_3(x)=\frac{\sqrt{2}}{x+1}\,\frac{x^3-9x^2+9x-1}{(x+1)^3}\, }[/math]

[math]\displaystyle{ R_4(x)=\frac{\sqrt{2}}{x+1}\,\frac{x^4-16x^3+36x^2-16x+1}{(x+1)^4}\, }[/math]

References

Zhong-Qing, Wang; Ben-Yu, Guo (2005). "A mixed spectral method for incompressible viscous fluid flow in an infinite strip". Mat. Apl. Comput. 24 (3). doi:10.1590/S0101-82052005000300002.