Line–sphere intersection
From HandWiki
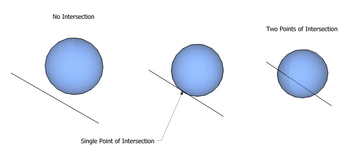
1. No intersection.
2. Point intersection.
3. Two point intersection.
In analytic geometry, a line and a sphere can intersect in three ways:
- No intersection at all
- Intersection in exactly one point
- Intersection in two points.
Methods for distinguishing these cases, and determining the coordinates for the points in the latter cases, are useful in a number of circumstances. For example, it is a common calculation to perform during ray tracing.[1]
Calculation using vectors in 3D
In vector notation, the equations are as follows:
Equation for a sphere
-
- : points on the sphere
- : center point
- : radius of the sphere
Equation for a line starting at
-
- : points on the line
- : origin of the line
- : distance from the origin of the line
- : direction of line (a non-zero vector)
Searching for points that are on the line and on the sphere means combining the equations and solving for , involving the dot product of vectors:
- Equations combined
- Expanded and rearranged:
- The form of a quadratic formula is now observable. (This quadratic equation is an instance of Joachimsthal's equation.[2])
- where
- Simplified
- Note that in the specific case where is a unit vector, and thus , we can simplify this further to (writing instead of to indicate a unit vector):
- If , then it is clear that no solutions exist, i.e. the line does not intersect the sphere (case 1).
- If , then exactly one solution exists, i.e. the line just touches the sphere in one point (case 2).
- If , two solutions exist, and thus the line touches the sphere in two points (case 3).
See also
- Intersection (geometry)
- Analytic geometry
- Line–plane intersection
- Plane–plane intersection
- Plane–sphere intersection
References
- ↑ Eberly, David H. (2006). 3D game engine design: a practical approach to real-time computer graphics, 2nd edition. Morgan Kaufmann.. p. 698. ISBN 0-12-229063-1.
- ↑ "Joachimsthal's Equation". http://mathworld.wolfram.com/JoachimsthalsEquation.html.
 |
