Dot product

Short description: Algebraic operation on coordinate vectors

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more).

Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. In modern geometry, Euclidean spaces are often defined by using vector spaces. In this case, the dot product is used for defining lengths (the length of a vector is the square root of the dot product of the vector by itself) and angles (the cosine of the angle between two vectors is the quotient of their dot product by the product of their lengths).

The name "dot product" is derived from the dot operator " · " that is often used to designate this operation; the alternative name "scalar product" emphasizes that the result is a scalar, rather than a vector (as with the vector product in three-dimensional space).

Definition

The dot product may be defined algebraically or geometrically. The geometric definition is based on the notions of angle and distance (magnitude) of vectors. The equivalence of these two definitions relies on having a Cartesian coordinate system for Euclidean space.

In modern presentations of Euclidean geometry, the points of space are defined in terms of their Cartesian coordinates, and Euclidean space itself is commonly identified with the real coordinate space [math]\displaystyle{ \mathbf{R}^n }[/math]. In such a presentation, the notions of length and angle are defined by means of the dot product. The length of a vector is defined as the square root of the dot product of the vector by itself, and the cosine of the (non oriented) angle between two vectors of length one is defined as their dot product. So the equivalence of the two definitions of the dot product is a part of the equivalence of the classical and the modern formulations of Euclidean geometry.

Coordinate definition

The dot product of two vectors [math]\displaystyle{ \mathbf{a} = [a_1, a_2, \cdots, a_n] }[/math] and [math]\displaystyle{ \mathbf{b} = [b_1, b_2, \cdots, b_n] }[/math], specified with respect to an orthonormal basis, is defined as:

[math]\displaystyle{ \mathbf a \cdot \mathbf b = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n }[/math]

where [math]\displaystyle{ \Sigma }[/math] denotes summation and [math]\displaystyle{ n }[/math] is the dimension of the vector space. For instance, in three-dimensional space, the dot product of vectors [math]\displaystyle{ [1,3,-5] }[/math] and [math]\displaystyle{ [4,-2,-1] }[/math] is:

[math]\displaystyle{ \begin{align} \ [1, 3, -5] \cdot [4, -2, -1] &= (1 \times 4) + (3\times-2) + (-5\times-1) \\ &= 4 - 6 + 5 \\ &= 3 \end{align} }[/math]

Likewise, the dot product of the vector [math]\displaystyle{ [1,3,-5] }[/math] with itself is:

[math]\displaystyle{ \begin{align} \ [1, 3, -5] \cdot [1, 3, -5] &= (1 \times 1) + (3\times 3) + (-5\times -5) \\ &= 1 + 9 + 25 \\ &= 35 \end{align} }[/math]

If vectors are identified with column vectors, the dot product can also be written as a matrix product

[math]\displaystyle{ \mathbf a \cdot \mathbf b = \mathbf a^{\mathsf T} \mathbf b, }[/math] where [math]\displaystyle{ a{^\mathsf T} }[/math] denotes the transpose of [math]\displaystyle{ \mathbf a }[/math].

Expressing the above example in this way, a 1 × 3 matrix (row vector) is multiplied by a 3 × 1 matrix (column vector) to get a 1 × 1 matrix that is identified with its unique entry: [math]\displaystyle{ \begin{bmatrix} 1 & 3 & -5 \end{bmatrix} \begin{bmatrix} 4 \\ -2 \\ -1 \end{bmatrix} = 3 \, . }[/math]

Geometric definition

Illustration showing how to find the angle between vectors using the dot product

Calculating bond angles of a symmetrical tetrahedral molecular geometry using a dot product

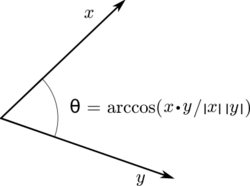
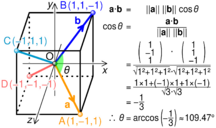
In Euclidean space, a Euclidean vector is a geometric object that possesses both a magnitude and a direction. A vector can be pictured as an arrow. Its magnitude is its length, and its direction is the direction to which the arrow points. The magnitude of a vector [math]\displaystyle{ \mathbf{a} }[/math] is denoted by [math]\displaystyle{ \left\| \mathbf{a} \right\| }[/math]. The dot product of two Euclidean vectors [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{b} }[/math] is defined by [math]\displaystyle{ \mathbf{a}\cdot\mathbf{b}= \left\|\mathbf{a}\right\| \left\|\mathbf{b}\right\|\cos\theta , }[/math] where [math]\displaystyle{ \theta }[/math] is the angle between [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{b} }[/math].

In particular, if the vectors [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{b} }[/math] are orthogonal (i.e., their angle is [math]\displaystyle{ \frac{\pi}{2} }[/math] or [math]\displaystyle{ 90^\circ }[/math]), then [math]\displaystyle{ \cos \frac \pi 2 = 0 }[/math], which implies that

[math]\displaystyle{ \mathbf a \cdot \mathbf b = 0 . }[/math] At the other extreme, if they are codirectional, then the angle between them is zero with [math]\displaystyle{ \cos 0 = 1 }[/math] and [math]\displaystyle{ \mathbf a \cdot \mathbf b = \left\| \mathbf a \right\| \, \left\| \mathbf b \right\| }[/math] This implies that the dot product of a vector [math]\displaystyle{ \mathbf{a} }[/math] with itself is [math]\displaystyle{ \mathbf a \cdot \mathbf a = \left\| \mathbf a \right\| ^2 , }[/math] which gives [math]\displaystyle{ \left\| \mathbf a \right\| = \sqrt{\mathbf a \cdot \mathbf a} , }[/math] the formula for the Euclidean length of the vector.

Scalar projection and first properties

Scalar projection

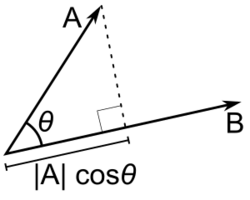
The scalar projection (or scalar component) of a Euclidean vector [math]\displaystyle{ \mathbf{a} }[/math] in the direction of a Euclidean vector [math]\displaystyle{ \mathbf{b} }[/math] is given by [math]\displaystyle{ a_b = \left\| \mathbf a \right\| \cos \theta , }[/math] where [math]\displaystyle{ \theta }[/math] is the angle between [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{b} }[/math].

In terms of the geometric definition of the dot product, this can be rewritten as [math]\displaystyle{ a_b = \mathbf a \cdot \widehat{\mathbf b} , }[/math] where [math]\displaystyle{ \widehat{\mathbf b} = \mathbf b / \left\| \mathbf b \right\| }[/math] is the unit vector in the direction of [math]\displaystyle{ \mathbf{b} }[/math].

Distributive law for the dot product

The dot product is thus characterized geometrically by [math]\displaystyle{ \mathbf a \cdot \mathbf b = a_b \left\| \mathbf{b} \right\| = b_a \left\| \mathbf{a} \right\| . }[/math] The dot product, defined in this manner, is homogeneous under scaling in each variable, meaning that for any scalar [math]\displaystyle{ \alpha }[/math], [math]\displaystyle{ ( \alpha \mathbf{a} ) \cdot \mathbf b = \alpha ( \mathbf a \cdot \mathbf b ) = \mathbf a \cdot ( \alpha \mathbf b ) . }[/math] It also satisfies the distributive law, meaning that [math]\displaystyle{ \mathbf a \cdot ( \mathbf b + \mathbf c ) = \mathbf a \cdot \mathbf b + \mathbf a \cdot \mathbf c . }[/math]

These properties may be summarized by saying that the dot product is a bilinear form. Moreover, this bilinear form is positive definite, which means that [math]\displaystyle{ \mathbf a \cdot \mathbf a }[/math] is never negative, and is zero if and only if [math]\displaystyle{ \mathbf a = \mathbf 0 }[/math], the zero vector.

Equivalence of the definitions

If [math]\displaystyle{ \mathbf{e}_1,\cdots,\mathbf{e}_n }[/math] are the standard basis vectors in [math]\displaystyle{ \mathbf{R}^n }[/math], then we may write [math]\displaystyle{ \begin{align} \mathbf a &= [a_1 , \dots , a_n] = \sum_i a_i \mathbf e_i \\ \mathbf b &= [b_1 , \dots , b_n] = \sum_i b_i \mathbf e_i. \end{align} }[/math] The vectors [math]\displaystyle{ \mathbf{e}_i }[/math] are an orthonormal basis, which means that they have unit length and are at right angles to each other. Since these vectors have unit length, [math]\displaystyle{ \mathbf e_i \cdot \mathbf e_i = 1 }[/math] and since they form right angles with each other, if [math]\displaystyle{ i\neq j }[/math], [math]\displaystyle{ \mathbf e_i \cdot \mathbf e_j = 0 . }[/math] Thus in general, we can say that: [math]\displaystyle{ \mathbf e_i \cdot \mathbf e_j = \delta_ {ij} , }[/math] where [math]\displaystyle{ \delta_{ij} }[/math] is the Kronecker delta.

Vector components in an orthonormal basis

Also, by the geometric definition, for any vector [math]\displaystyle{ \mathbf{e}_i }[/math] and a vector [math]\displaystyle{ \mathbf{a} }[/math], we note that [math]\displaystyle{ \mathbf a \cdot \mathbf e_i = \left\| \mathbf a \right\| \, \left\| \mathbf e_i \right\| \cos \theta_i = \left\| \mathbf a \right\| \cos \theta_i = a_i , }[/math] where [math]\displaystyle{ a_i }[/math] is the component of vector [math]\displaystyle{ \mathbf{a} }[/math] in the direction of [math]\displaystyle{ \mathbf{e}_i }[/math]. The last step in the equality can be seen from the figure.

Now applying the distributivity of the geometric version of the dot product gives [math]\displaystyle{ \mathbf a \cdot \mathbf b = \mathbf a \cdot \sum_i b_i \mathbf e_i = \sum_i b_i ( \mathbf a \cdot \mathbf e_i ) = \sum_i b_i a_i= \sum_i a_i b_i , }[/math] which is precisely the algebraic definition of the dot product. So the geometric dot product equals the algebraic dot product.

Properties

The dot product fulfills the following properties if [math]\displaystyle{ \mathbf{a} }[/math], [math]\displaystyle{ \mathbf{b} }[/math], and [math]\displaystyle{ \mathbf{c} }[/math] are real vectors and [math]\displaystyle{ r }[/math], [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math] are scalars.

Commutative

[math]\displaystyle{ \mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a} , }[/math] which follows from the definition ([math]\displaystyle{ \theta }[/math] is the angle between [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{b} }[/math]): [math]\displaystyle{ \mathbf{a} \cdot \mathbf{b} = \left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \cos \theta = \left\| \mathbf{b} \right\| \left\| \mathbf{a} \right\| \cos \theta = \mathbf{b} \cdot \mathbf{a} . }[/math]

Distributive over vector addition

[math]\displaystyle{ \mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c} . }[/math]

Bilinear

[math]\displaystyle{ \mathbf{a} \cdot ( r \mathbf{b} + \mathbf{c} ) = r ( \mathbf{a} \cdot \mathbf{b} ) + ( \mathbf{a} \cdot \mathbf{c} ) . }[/math]

Scalar multiplication

[math]\displaystyle{ ( c_1 \mathbf{a} ) \cdot ( c_2 \mathbf{b} ) = c_1 c_2 ( \mathbf{a} \cdot \mathbf{b} ) . }[/math]

Not associative

because the dot product between a scalar [math]\displaystyle{ \mathbf{a}\cdot\mathbf{b} }[/math] and a vector [math]\displaystyle{ \mathbf{c} }[/math] is not defined, which means that the expressions involved in the associative property, [math]\displaystyle{ (\mathbf{a}\cdot\mathbf{b})\cdot\mathbf{c} }[/math] or [math]\displaystyle{ \mathbf{a}\cdot(\mathbf{b}\cdot\mathbf{c}) }[/math] are both ill-defined. Note however that the previously mentioned scalar multiplication property is sometimes called the "associative law for scalar and dot product" or one can say that "the dot product is associative with respect to scalar multiplication" because [math]\displaystyle{ c (\mathbf{a} \cdot \mathbf{b}) = (c\mathbf{a})\cdot\mathbf{b} = \mathbf{a}\cdot(c\mathbf{b}) }[/math].

Orthogonal

Two non-zero vectors [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{b} }[/math] are orthogonal if and only if [math]\displaystyle{ \mathbf{a} \cdot \mathbf{b} = 0 }[/math].

No cancellation

Unlike multiplication of ordinary numbers, where if [math]\displaystyle{ ab=ac }[/math], then [math]\displaystyle{ b }[/math] always equals [math]\displaystyle{ c }[/math] unless [math]\displaystyle{ a }[/math] is zero, the dot product does not obey the cancellation law:

If [math]\displaystyle{ \mathbf{a}\cdot\mathbf{b}=\mathbf{a}\cdot\mathbf{c} }[/math] and [math]\displaystyle{ \mathbf{a}\neq\mathbf{0} }[/math], then we can write: [math]\displaystyle{ \mathbf{a}\cdot(\mathbf{b}-\mathbf{c}) = 0 }[/math] by the distributive law; the result above says this just means that [math]\displaystyle{ \mathbf{a} }[/math] is perpendicular to [math]\displaystyle{ (\mathbf{b}-\mathbf{c}) }[/math], which still allows [math]\displaystyle{ (\mathbf{b}-\mathbf{c})\neq\mathbf{0} }[/math], and therefore allows [math]\displaystyle{ \mathbf{b}\neq\mathbf{c} }[/math].

Product rule

If [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{b} }[/math] are vector-valued differentiable functions, then the derivative (denoted by a prime [math]\displaystyle{ {}' }[/math]) of [math]\displaystyle{ \mathbf{a}\cdot\mathbf{b} }[/math] is given by the rule [math]\displaystyle{ (\mathbf{a}\cdot\mathbf{b})' = \mathbf{a}'\cdot\mathbf{b} + \mathbf{a}\cdot\mathbf{b}'. }[/math]

Application to the law of cosines

Triangle with vector edges a and b, separated by angle θ.

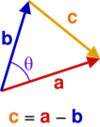
Given two vectors [math]\displaystyle{ {\color{red}\mathbf{a}} }[/math] and [math]\displaystyle{ {\color{blue}\mathbf{b}} }[/math] separated by angle [math]\displaystyle{ \theta }[/math] (see image right), they form a triangle with a third side [math]\displaystyle{ {\color{orange}\mathbf{c}} = {\color{red}\mathbf{a}} - {\color{blue}\mathbf{b}} }[/math]. Let [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math] denote the lengths of [math]\displaystyle{ {\color{red}\mathbf{a}} }[/math], [math]\displaystyle{ {\color{blue}\mathbf{b}} }[/math], and [math]\displaystyle{ {\color{orange}\mathbf{c}} }[/math], respectively. The dot product of this with itself is:

[math]\displaystyle{ \begin{align} \mathbf{\color{orange}c} \cdot \mathbf{\color{orange}c} & = ( \mathbf{\color{red}a} - \mathbf{\color{blue}b}) \cdot ( \mathbf{\color{red}a} - \mathbf{\color{blue}b} ) \\ & = \mathbf{\color{red}a} \cdot \mathbf{\color{red}a} - \mathbf{\color{red}a} \cdot \mathbf{\color{blue}b} - \mathbf{\color{blue}b} \cdot \mathbf{\color{red}a} + \mathbf{\color{blue}b} \cdot \mathbf{\color{blue}b} \\ & = {\color{red}a}^2 - \mathbf{\color{red}a} \cdot \mathbf{\color{blue}b} - \mathbf{\color{red}a} \cdot \mathbf{\color{blue}b} + {\color{blue}b}^2 \\ & = {\color{red}a}^2 - 2 \mathbf{\color{red}a} \cdot \mathbf{\color{blue}b} + {\color{blue}b}^2 \\ {\color{orange}c}^2 & = {\color{red}a}^2 + {\color{blue}b}^2 - 2 {\color{red}a} {\color{blue}b} \cos \mathbf{\color{purple}\theta} \\ \end{align} }[/math]

which is the law of cosines.

Triple product

There are two ternary operations involving dot product and cross product.

The scalar triple product of three vectors is defined as [math]\displaystyle{ \mathbf{a} \cdot ( \mathbf{b} \times \mathbf{c} ) = \mathbf{b} \cdot ( \mathbf{c} \times \mathbf{a} )=\mathbf{c} \cdot ( \mathbf{a} \times \mathbf{b} ). }[/math] Its value is the determinant of the matrix whose columns are the Cartesian coordinates of the three vectors. It is the signed volume of the parallelepiped defined by the three vectors, and is isomorphic to the three-dimensional special case of the exterior product of three vectors.

The vector triple product is defined by [math]\displaystyle{ \mathbf{a} \times ( \mathbf{b} \times \mathbf{c} ) = ( \mathbf{a} \cdot \mathbf{c} )\, \mathbf{b} - ( \mathbf{a} \cdot \mathbf{b} )\, \mathbf{c} . }[/math] This identity, also known as Lagrange's formula, may be remembered as "ACB minus ABC", keeping in mind which vectors are dotted together. This formula has applications in simplifying vector calculations in physics.

Physics

In physics, vector magnitude is a scalar in the physical sense (i.e., a physical quantity independent of the coordinate system), expressed as the product of a numerical value and a physical unit, not just a number. The dot product is also a scalar in this sense, given by the formula, independent of the coordinate system. For example:

• Mechanical work is the dot product of force and displacement vectors,
• Power is the dot product of force and velocity.

Generalizations

Complex vectors

For vectors with complex entries, using the given definition of the dot product would lead to quite different properties. For instance, the dot product of a vector with itself could be zero without the vector being the zero vector (e.g. this would happen with the vector [math]\displaystyle{ \mathbf{a} = [1\ i] }[/math]). This in turn would have consequences for notions like length and angle. Properties such as the positive-definite norm can be salvaged at the cost of giving up the symmetric and bilinear properties of the dot product, through the alternative definition [math]\displaystyle{ \mathbf{a} \cdot \mathbf{b} = \sum_i {{a_i}\,\overline{b_i}} , }[/math] where [math]\displaystyle{ \overline{b_i} }[/math] is the complex conjugate of [math]\displaystyle{ b_i }[/math]. When vectors are represented by column vectors, the dot product can be expressed as a matrix product involving a conjugate transpose, denoted with the superscript H:

[math]\displaystyle{ \mathbf{a} \cdot \mathbf{b} = \mathbf{b}^\mathsf{H} \mathbf{a} . }[/math]

In the case of vectors with real components, this definition is the same as in the real case. The dot product of any vector with itself is a non-negative real number, and it is nonzero except for the zero vector. However, the complex dot product is sesquilinear rather than bilinear, as it is conjugate linear and not linear in [math]\displaystyle{ \mathbf{a} }[/math]. The dot product is not symmetric, since [math]\displaystyle{ \mathbf{a} \cdot \mathbf{b} = \overline{\mathbf{b} \cdot \mathbf{a}} . }[/math] The angle between two complex vectors is then given by [math]\displaystyle{ \cos \theta = \frac{\operatorname{Re} ( \mathbf{a} \cdot \mathbf{b} )}{ \left\| \mathbf{a} \right\| \, \left\| \mathbf{b} \right\| } . }[/math]

The complex dot product leads to the notions of Hermitian forms and general inner product spaces, which are widely used in mathematics and physics.

The self dot product of a complex vector [math]\displaystyle{ \mathbf{a} \cdot \mathbf{a} = \mathbf{a}^\mathsf{H} \mathbf{a} }[/math], involving the conjugate transpose of a row vector, is also known as the norm squared, [math]\displaystyle{ \mathbf{a} \cdot \mathbf{a} = \|\mathbf{a}\|^2 }[/math], after the Euclidean norm; it is a vector generalization of the absolute square of a complex scalar (see also: squared Euclidean distance).

Inner product

The inner product generalizes the dot product to abstract vector spaces over a field of scalars, being either the field of real numbers [math]\displaystyle{ \R }[/math] or the field of complex numbers [math]\displaystyle{ \Complex }[/math]. It is usually denoted using angular brackets by [math]\displaystyle{ \left\langle \mathbf{a} \, , \mathbf{b} \right\rangle }[/math].

The inner product of two vectors over the field of complex numbers is, in general, a complex number, and is sesquilinear instead of bilinear. An inner product space is a normed vector space, and the inner product of a vector with itself is real and positive-definite.

Functions

The dot product is defined for vectors that have a finite number of entries. Thus these vectors can be regarded as discrete functions: a length-[math]\displaystyle{ n }[/math] vector [math]\displaystyle{ u }[/math] is, then, a function with domain [math]\displaystyle{ \{k\in\mathbb{N}:1\leq k \leq n\} }[/math], and [math]\displaystyle{ u_i }[/math] is a notation for the image of [math]\displaystyle{ i }[/math] by the function/vector [math]\displaystyle{ u }[/math].

This notion can be generalized to continuous functions: just as the inner product on vectors uses a sum over corresponding components, the inner product on functions is defined as an integral over some interval [a, b]:

[math]\displaystyle{ \left\langle u , v \right\rangle = \int_a^b u(x) v(x) \,dx. }[/math]

Generalized further to complex functions [math]\displaystyle{ \psi(x) }[/math] and [math]\displaystyle{ \chi(x) }[/math], by analogy with the complex inner product above, gives

[math]\displaystyle{ \left\langle \psi , \chi \right\rangle = \int_a^b \psi(x) \overline{\chi(x)} \,dx. }[/math]

Weight function

Inner products can have a weight function (i.e., a function which weights each term of the inner product with a value). Explicitly, the inner product of functions [math]\displaystyle{ u(x) }[/math] and [math]\displaystyle{ v(x) }[/math] with respect to the weight function [math]\displaystyle{ r(x)\gt 0 }[/math] is

[math]\displaystyle{ \left\langle u , v \right\rangle_r = \int_a^b r(x) u(x) v(x) \, d x. }[/math]

Dyadics and matrices

A double-dot product for matrices is the Frobenius inner product, which is analogous to the dot product on vectors. It is defined as the sum of the products of the corresponding components of two matrices [math]\displaystyle{ \mathbf{A} }[/math] and [math]\displaystyle{ \mathbf{B} }[/math] of the same size:

[math]\displaystyle{ \mathbf{A} : \mathbf{B} = \sum_i \sum_j A_{ij} \overline{B_{ij}} = \operatorname{tr} ( \mathbf{B}^\mathsf{H} \mathbf{A} ) = \operatorname{tr} ( \mathbf{A} \mathbf{B}^\mathsf{H} ) . }[/math] And for real matrices, [math]\displaystyle{ \mathbf{A} : \mathbf{B} = \sum_i \sum_j A_{ij} B_{ij} = \operatorname{tr} ( \mathbf{B}^\mathsf{T} \mathbf{A} ) = \operatorname{tr} ( \mathbf{A} \mathbf{B}^\mathsf{T} ) = \operatorname{tr} ( \mathbf{A}^\mathsf{T} \mathbf{B} ) = \operatorname{tr} ( \mathbf{B} \mathbf{A}^\mathsf{T} ) . }[/math]

Writing a matrix as a dyadic, we can define a different double-dot product (see Dyadics § Product of dyadic and dyadic) however it is not an inner product.

Tensors

The inner product between a tensor of order [math]\displaystyle{ n }[/math] and a tensor of order [math]\displaystyle{ m }[/math] is a tensor of order [math]\displaystyle{ n+m-2 }[/math], see Tensor contraction for details.

Computation

Algorithms

The straightforward algorithm for calculating a floating-point dot product of vectors can suffer from catastrophic cancellation. To avoid this, approaches such as the Kahan summation algorithm are used.

Libraries

A dot product function is included in:

• BLAS level 1 real SDOT, DDOT; complex CDOTU, ZDOTU = X^T * Y, CDOTC, ZDOTC = X^H * Y
• Fortran as dot_product(A,B) or sum(conjg(A) * B)
• Julia as  A' * B or standard library LinearAlgebra as dot(A, B)
• R (programming language) as sum(A * B) for vectors or, more generally for matrices, as A %*% B
• Matlab as  A' * B  or  conj(transpose(A)) * B  or  sum(conj(A) .* B)  or  dot(A, B)
• Python (package NumPy) as  numpy.dot(A, B)  or  numpy.inner(A, B)
• GNU Octave as  sum(conj(X) .* Y, dim), and similar code as Matlab
• Intel oneAPI Math Kernel Library real p?dot dot = sub(x)'*sub(y); complex p?dotc dotc = conjg(sub(x)')*sub(y)

See also

• Cauchy–Schwarz inequality
• Cross product
• Dot product representation of a graph
• Euclidean norm, the square-root of the self dot product
• Matrix multiplication
• Metric tensor
• Multiplication of vectors
• Outer product

External links

• Hazewinkel, Michiel, ed. (2001), "Inner product", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/i051240 
• Explanation of dot product including with complex vectors
• "Dot Product" by Bruce Torrence, Wolfram Demonstrations Project, 2007.