Linear interpolation
In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points.
Linear interpolation between two known points
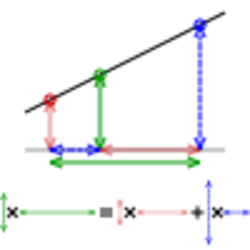
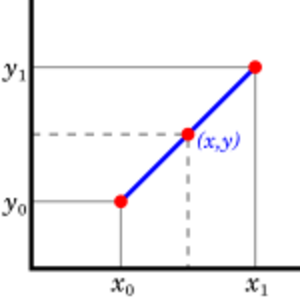
If the two known points are given by the coordinates and , the linear interpolant is the straight line between these points. For a value in the interval , the value along the straight line is given from the equation of slopes which can be derived geometrically from the figure on the right. It is a special case of polynomial interpolation with .
Solving this equation for , which is the unknown value at , gives which is the formula for linear interpolation in the interval . Outside this interval, the formula is identical to linear extrapolation.
This formula can also be understood as a weighted average. The weights are inversely related to the distance from the end points to the unknown point; the closer point has more influence than the farther point. Thus, the weights are and , which are normalized distances between the unknown point and each of the end points. Because these sum to 1, yielding the formula for linear interpolation given above.
Interpolation of a data set
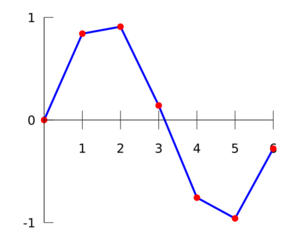
Linear interpolation on a set of data points (x0, y0), (x1, y1), ..., (xn, yn) is defined as piecewise linear, resulting from the concatenation of linear segment interpolants between each pair of data points. This results in a continuous curve, with a discontinuous derivative (in general), thus of differentiability class .
Linear interpolation as an approximation
Linear interpolation is often used to approximate a value of some function f using two known values of that function at other points. The error of this approximation is defined as where p denotes the linear interpolation polynomial defined above:
It can be proven using Rolle's theorem that if f has a continuous second derivative, then the error is bounded by
That is, the approximation between two points on a given function gets worse with the second derivative of the function that is approximated. This is intuitively correct as well: the "curvier" the function is, the worse the approximations made with simple linear interpolation become.
History and applications
Linear interpolation has been used since antiquity for filling the gaps in tables. Suppose that one has a table listing the population of some country in 1970, 1980, 1990 and 2000, and that one wanted to estimate the population in 1994. Linear interpolation is an easy way to do this. It is believed that it was used in the Seleucid Empire (last three centuries BC) and by the Greek astronomer and mathematician Hipparchus (second century BC). A description of linear interpolation can be found in the ancient Chinese mathematical text called The Nine Chapters on the Mathematical Art (九章算術),[1] dated from 200 BC to AD 100 and the Almagest (2nd century AD) by Ptolemy.
The basic operation of linear interpolation between two values is commonly used in computer graphics. In that field's jargon it is sometimes called a lerp (from linear interpolation). The term can be used as a verb or noun for the operation. e.g. "Bresenham's algorithm lerps incrementally between the two endpoints of the line."
Lerp operations are built into the hardware of all modern computer graphics processors. They are often used as building blocks for more complex operations: for example, a bilinear interpolation can be accomplished in three lerps. Because this operation is cheap, it's also a good way to implement accurate lookup tables with quick lookup for smooth functions without having too many table entries.
Extensions
Accuracy
If a C0 function is insufficient, for example if the process that has produced the data points is known to be smoother than C0, it is common to replace linear interpolation with spline interpolation or, in some cases, polynomial interpolation.
Multivariate
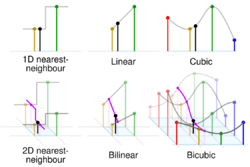
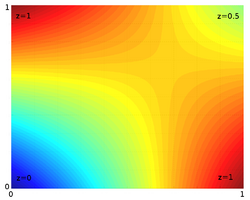
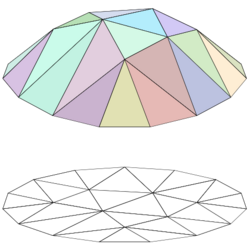
Linear interpolation as described here is for data points in one spatial dimension. For two spatial dimensions, the extension of linear interpolation is called bilinear interpolation, and in three dimensions, trilinear interpolation. Notice, though, that these interpolants are no longer linear functions of the spatial coordinates, rather products of linear functions; this is illustrated by the clearly non-linear example of bilinear interpolation in the figure below. Other extensions of linear interpolation can be applied to other kinds of mesh such as triangular and tetrahedral meshes, including Bézier surfaces. These may be defined as indeed higher-dimensional piecewise linear functions (see second figure below).
Programming language support
Many libraries and shading languages have a "lerp" helper-function (in GLSL known instead as mix), returning an interpolation between two inputs (v0, v1) for a parameter t in the closed unit interval [0, 1]. Signatures between lerp functions are variously implemented in both the forms (v0, v1, t) and (t, v0, v1).
// Imprecise method, which does not guarantee v = v1 when t = 1, due to floating-point arithmetic error.
// This method is monotonic. This form may be used when the hardware has a native fused multiply-add instruction.
float lerp(float v0, float v1, float t) {
return v0 + t * (v1 - v0);
}
// Precise method, which guarantees v = v1 when t = 1. This method is monotonic only when v0 * v1 < 0.
// Lerping between same values might not produce the same value
float lerp(float v0, float v1, float t) {
return (1 - t) * v0 + t * v1;
}
This lerp function is commonly used for alpha blending (the parameter "t" is the "alpha value"), and the formula may be extended to blend multiple components of a vector (such as spatial x, y, z axes or r, g, b colour components) in parallel.
See also
- Bilinear interpolation
- Spline interpolation
- Polynomial interpolation
- de Casteljau's algorithm
- First-order hold
- Bézier curve
References
- ↑ Joseph Needham (1 January 1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. pp. 147–. ISBN 978-0-521-05801-8. https://books.google.com/books?id=jfQ9E0u4pLAC&pg=PA147.
- Meijering, Erik (2002), "A chronology of interpolation: from ancient astronomy to modern signal and image processing", Proceedings of the IEEE 90 (3): 319–342, doi:10.1109/5.993400, http://infoscience.epfl.ch/record/63085.
External links
- Equations of the Straight Line at cut-the-knot
- Well-behaved interpolation for numbers and pointers
- Hazewinkel, Michiel, ed. (2001), "Linear interpolation", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/l059330
- Hazewinkel, Michiel, ed. (2001), "Finite-increments formula", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/f040300
- Lerp smoothing is broken - a journey of decay and delta time
de:Interpolation (Mathematik)#Lineare Interpolation
 |
