Locating the center of mass
There are several methods for locating the center of mass of a body.
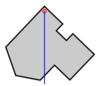
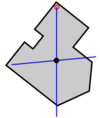
Plumb lines
This method is useful when one wishes to find the centroid of a complex planar shape with unknown dimensions. It relies on finding the center of mass of a thin body of homogeneous density having the same shape as the complex planar shape.
 |
 |
 |
| Step 1: An arbitrary 2-D shape. | Step 2: Suspend the shape from a location near an edge. Drop a plumb line and mark on the object. | Step 3: Suspend the shape from another location not too close to the first. Drop a plumb line again and mark. The intersection of the two lines is the center of mass. |
Subdivision
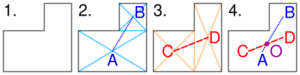
Of an L-shaped object
This is a method of determining the center of mass of an L-shaped object.
- Divide the shape into two rectangles, as shown in fig 2. Find the center of masses of these two rectangles by drawing the diagonals. Draw a line joining the centers of mass. The center of mass of the shape must lie on this line AB.
- Divide the shape into two other rectangles, as shown in fig 3. Find the centers of mass of these two rectangles by drawing the diagonals. Draw a line joining the centers of mass. The center of mass of the L-shape must lie on this line CD.
- As the center of mass of the shape must lie along AB and also along CD, it is obvious that it is at the intersection of these two lines, at O. (The point O may or may not lie inside the L-shaped object.)
Of a composite shape
This method is useful when one wishes to find the location of the centroid or center of mass of an object that is easily divided into elementary shapes, whose centers of mass are easy to find (see List of centroids). Here the center of mass will only be found in the x direction. The same procedure may be followed to locate the center of mass in the y direction.
The shape. It is easily divided into a square, triangle, and circle. Note that the circle will have negative area. From the List of centroids, we note the coordinates of the individual centroid. From equation 1 above:
[math]\displaystyle{ \frac{3 \times (-2.5^2\pi) + 5 \times 10^2 + 13.33 \times \frac{10^2}{2}}{ -2.5^2\pi + 10^2 + \frac{10^2}{2}} \approx 8.5 }[/math] units.
The center of mass of this figure is at a distance of 8.5 units from the left corner of the figure.
Tracing the perimeter
A direct development of the planimeter known as an integraph, or integerometer (though a better term is probably moment planimeter), can be used to establish the position of the centroid or center of mass of an irregular shape. This method can be applied to a shape with an irregular, smooth or complex boundary where other methods are too difficult. It was regularly used by ship builders to ensure the ship would not capsize. See Locating the center of mass by mechanical means.
See also
References
 |
