Lochs's theorem

Short description: On the rate of convergence of the continued fraction expansion of a typical real number

In number theory, Lochs's theorem concerns the rate of convergence of the continued fraction expansion of a typical real number. A proof of the theorem was published in 1964 by Gustav Lochs.

The theorem states that for almost all real numbers in the interval (0,1), the number of terms m of the number's continued fraction expansion that are required to determine the first n places of the number's decimal expansion behaves asymptotically as follows:

[math]\displaystyle{ \lim_{n\to\infty}\frac{m}{n}=\frac{6\ln(2)\ln(10)}{\pi^2} \approx 0.97027014 }[/math] (sequence A086819 in the OEIS).

As this limit is only slightly smaller than 1, this can be interpreted as saying that each additional term in the continued fraction representation of a "typical" real number increases the accuracy of the representation by approximately one decimal place. The decimal system is the last positional system for which each digit carries less information than one continued fraction quotient; going to base-11 (changing [math]\displaystyle{ \ln(10) }[/math] to [math]\displaystyle{ \ln(11) }[/math] in the equation) makes the above value exceed 1.

The reciprocal of this limit,

[math]\displaystyle{ \frac{\pi^2}{6\ln(2)\ln(10)} \approx 1.03064083 }[/math] (sequence A062542 in the OEIS),

is twice the base-10 logarithm of Lévy's constant.

Three typical numbers, and the golden ratio. The typical numbers follow an approximately 45° line, since each continued fraction coefficient yields approximately one decimal digit. The golden ratio, on the other hand, is the number requiring the most coefficients for each digit.

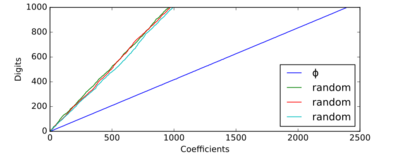
A prominent example of a number not exhibiting this behavior is the golden ratio—sometimes known as the "most irrational" number—whose continued fraction terms are all ones, the smallest possible in canonical form. On average it requires approximately 2.39 continued fraction terms per decimal digit.

Proof

The proof assumes basic properties of continued fractions. Let [math]\displaystyle{ T : x \mapsto 1/x \mod 1 }[/math] be the Gauss map.

Let [math]\displaystyle{ \rho(t) = \frac{1}{(1+t)\ln 2} }[/math] be the probability density function for the Gauss distribution, which is preserved under the Gauss map.

Since the probability density function is bounded above and below, a set is negligible with respect to the Lebesgue measure iff to the Gauss distribution.

Lemma

Lemma. [math]\displaystyle{ \frac 1n \ln T^n x \to 0 }[/math].

Proof. Since [math]\displaystyle{ T^nx \leq 1 }[/math], we have [math]\displaystyle{ \frac 1n \ln T^n x \to 0 }[/math] iff[math]\displaystyle{ \liminf\frac 1n \ln T^n x = 0 }[/math]Let us consider the set of all [math]\displaystyle{ x }[/math] that have [math]\displaystyle{ \liminf\frac 1n \ln T^n x \lt 0 }[/math]. That is,[math]\displaystyle{ \{x : \exists c \gt 0, \forall N \geq 1, \exists n \geq N, T^n x \lt e^{-cn}\} }[/math] [math]\displaystyle{ = \cup_{c \gt 0} \cap_{N \geq 1} \cup_{n \geq N} [0; \N, \dots, \N, a_n \gt e^{cn}, \N, \dots] }[/math]where [math]\displaystyle{ [0; \N, \dots, \N, a_n \gt e^{cn}, \N, \dots] }[/math] denotes the set of numbers whose continued fraction expansion has [math]\displaystyle{ a_n \gt e^{cn} }[/math], but no other constraints. Now, since the Gauss map preserves the Gauss measure,[math]\displaystyle{ [0; \N, \dots, \N, a_n \gt e^{cn}, \N, \dots] }[/math]has the same Gauss measure as [math]\displaystyle{ [0; a_n \gt e^{cn}, \N, \dots] }[/math], which is the same as

[math]\displaystyle{ \int_0^{e^{-cn}} \rho(t)dt = \log_2(1+e^{-cn})\sim \frac{e^{-cn}}{\ln 2} }[/math]The union over [math]\displaystyle{ \cup_{n \geq N} }[/math] sums to [math]\displaystyle{ \sim \frac{e^{-cN}}{(1-e^{-c})\ln 2} }[/math], which at the [math]\displaystyle{ N\to\infty }[/math] limit is zero.

Thus the set of such [math]\displaystyle{ x }[/math] has Gauss measure zero.

Finish the estimate

Now, expand the term using basic continued fraction properties:[math]\displaystyle{ \ln\left| x - \frac{p_n}{q_n} \right| = \ln \frac{T^n x}{q_n(q_n + q_{n-1}T^n x )} = - 2\ln q_n + \ln T^n x - \ln\left(1 + \frac{q_{n-1}}{q_n}T^n x \right) }[/math]The second is [math]\displaystyle{ o(n) }[/math]. The third term is [math]\displaystyle{ \in [\ln 1, \ln 2] }[/math]. Both disappear after dividing by [math]\displaystyle{ n }[/math].
Thus[math]\displaystyle{ \lim_{n} \frac 1n \ln\left| x - \frac{p_n}{q_n} \right| = -2 \lim_n \frac 1n \ln q_n = -\frac{\pi^2}{6\ln 2} }[/math]where we used the result from Lévy's constant.