Lune (geometry)

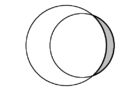
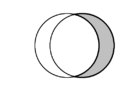
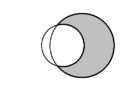
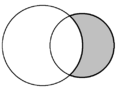
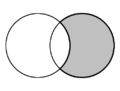
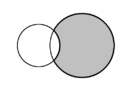
In plane geometry, the crescent shape formed by two intersecting circles is called a lune. In each diagram, two lunes are present, and one is shaded in grey.

In plane geometry, a lune is the concave-convex region bounded by two circular arcs. It has one boundary portion for which the connecting segment of any two nearby points moves outside the region and another boundary portion for which the connecting segment of any two nearby points lies entirely inside the region. A convex-convex region is termed a lens. The word lune derives from luna, the Latin word for "moon".

Formally, a lune is the relative complement of one disk in another (where they intersect but neither is a subset of the other). Alternatively, if [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are disks, then [math]\displaystyle{ A - A \cap B }[/math] is a lune.

Squaring the lune

In the 5th century BC, Hippocrates of Chios showed that Lune of Hippocrates and two other lunes could be exactly squared (converted into a square having the same area) by straightedge and compass. In the 19th century two more squarable lunes were found, and in the 20th century it was shown that these five are the only squarable lunes.

Area

The area of a lune formed by circles of radii a and b (b>a) with distance c between their centers is

[math]\displaystyle{ A=2\Delta+a^2\sec^{-1}\left(\frac{2ac}{b^2-a^2-c^2}\right)-b^2\sec^{-1}\left(\frac{2bc}{b^2+c^2-a^2}\right), }[/math]

where [math]\displaystyle{ \text{sec}^{-1} }[/math] is the inverse function of the secant function, and where

[math]\displaystyle{ \Delta= \frac{1}{4} \sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)} }[/math]

is the area of a triangle with sides a, b and c.

See also

• Arbelos
• Crescent
• Gauss–Bonnet theorem

External links

• The Five Squarable Lunes at MathPages