Medicine:Wave intensity analysis

Short description: Method in the dynamics of blood flow

Figure 1. The pressure and velocity measured in the ascending aorta in an elderly man.

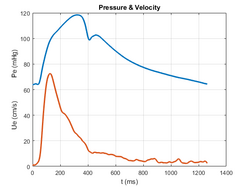
Wave intensity analysis provides a method to calculate the properties of arterial waves that give rise to arterial blood pressure, based on measurements of pressure, P, and velocity, U, waveforms (Figure 1). Wave intensity analysis is applicable to the evaluation of circulatory physiology and quantifying the pathophysiology of disorders such as coronary artery disease. The method is based on discrete, successive wave fronts (wavelets) and is carried out in the time domain. These wavelets travel forward and backwards in the arteries with amplitudes [math]\displaystyle{ \Delta P }[/math] and [math]\displaystyle{ \Delta U }[/math]. The wave intensity, [math]\displaystyle{ \Delta I }[/math], of a particular wavelet is defined as[math]\displaystyle{ \Delta I = \Delta P\Delta U }[/math]It is related to sound intensity in acoustics and describes the power per unit area carried by the wavelet. From the theory discussed below, there is a relationship between the pressure amplitude and the velocity amplitude of a wavelet[math]\displaystyle{ \Delta P_\pm = \frac{1}{2} (\Delta P_\pm \pm \rho c \Delta U_\pm) }[/math]where ρ is the density of blood and c is the wave speed of the wavelet. From these equations, generally known as the water hammer equations, it follows that the wave intensity for forward wavelets [math]\displaystyle{ \Delta I_+ \gt 0 }[/math] and for backward wavelets [math]\displaystyle{ \Delta I_- \lt 0 }[/math]. The ability to determine the direction of a wavelet from its sign is the basis of the practical utility of wave intensity analysis.

Figure 2. The wave intensity calculated from the measured pressure and velocity measured in the ascending aorta of an elderly man.

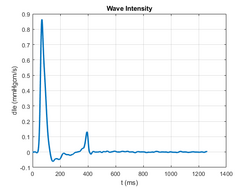
Net wave intensity

The pressure amplitude of a wavelet can be positive (compression) or negative (decompression) and the velocity amplitude can be positive (acceleration) or negative (deceleration). The measured changes [math]\displaystyle{ \Delta P }[/math] and [math]\displaystyle{ \Delta U }[/math] are the sums of the amplitudes of the forward and backward wavelets arriving at the measurement site at the time of the measurement and so the wave intensity [math]\displaystyle{ \Delta I }[/math] is sometimes called net wave intensity. The [math]\displaystyle{ \Delta I }[/math] in the Figure 2 shows the normal pattern in the aorta and illustrates four important features:

1. A large positive peak at the start of systole indicating a dominant forward wave due to the compression of the left ventricle.
2. A period of relatively small negative wave intensity during mid-systole indicating a small level of reflected wave activity.
3. A smaller positive peak at the end of systole indicating that the deceleration of blood at the end of systole is predominantly due to a forward deceleration wave instead of backward reflected waves.
4. The very low level of net wave intensity during diastole

Departures from this pattern of wave intensity is usually indicative of pathology.

Figure 3. The pressure (minus the diastolic pressure) measured in the ascending aorta of an elderly man separated into the forward and backward pressures using wave intensity analysis.

Separation of forward and backward waves

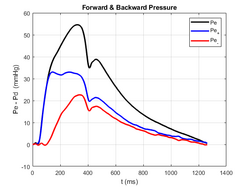
The additivity of the forward and backward wavelets coinciding at the site of measurement at a particular time can be combined algebraically with the water-hammer equations to calculate the magnitudes of the two wavelets[math]\displaystyle{ \Delta P_\pm = \frac{1}{2} (\Delta P_\pm \pm \rho c \Delta U_\pm) }[/math]This method assumes that the wave speed is constant. In general, the wave speed is a function of the pressure. A more complex method of separation involving integrals along the characteristics is available. The forward and backward waveforms follow from summing the magnitudes of the sequential wavelets[math]\displaystyle{ P_\pm = \Sigma \Delta P_\pm }[/math]The pressure shown in Figure 1 is separated into its forward and backward components in Figure 3. This separation is carried out in the time domain and can be applied to irregular, non-periodic data. For periodic heart beats this separation coincides closely with the separation obtained using Fourier analysis methods.

Theoretical basis of wave intensity analysis

Wave intensity analysis is based on the 1-D equations for the conservation of mass and momentum of the blood in the elastic arteries (first published by Euler in 1775) and a relationship between the cross-sectional area of the artery and the pressure within it (generally called a 'tube law'). The resultant equations are hyperbolic in form and can be solved using the method of characteristics. The method is based on the identification of 'characteristic' directions along which the partial differential equations reduce to ordinary differential equations. For the arteries these characteristic directions were ([math]\displaystyle{ x \pm ct }[/math]) where [math]\displaystyle{ c }[/math] is the wave speed[math]\displaystyle{ c = \frac{1}{\sqrt{\rho \mathcal{D}} } }[/math]where [math]\displaystyle{ \mathcal{D} = \frac{1}{A} \frac{dA}{dP} }[/math] is the distensibility of the artery wall. These characteristic directions describe the path of the wavelets in [math]\displaystyle{ (x,t) }[/math]. The derivation of an equation for the local wave speed is a significant advantage of the method of characteristics.

Practical estimation of the local wave speed

A method for estimating local wave speed from clinically measurable data is important in wave intensity analysis. The most common approach is referred to as the 'P-U loop' method. During the initial compression wave at the start of systole when the forward wave is dominant the local wave speed is estimated from the slope of the P-U loop[math]\displaystyle{ c \approx \frac{1}{\rho} \left| \frac{dP}{dU} \right|_{initial \; systole} }[/math]In cases where there is no period during the cardiac cycle when it is obvious that forward waves dominate another method, generally called the 'sum of squares' method is applicable:[math]\displaystyle{ c \approx \frac{1}{\rho} \sqrt{\frac{\Sigma \Delta P^2}{\Sigma \Delta U^2} } }[/math]Here the sums are taken over a complete cardiac period. This estimation has been used extensively in the wave intensity analysis of measurements in the coronary arteries. It should be remembered that both of these estimates are approximations and should be used with caution.

Variants of wave intensity analysis

Wave intensity analysis was developed at an era when intra-arterial pressure and velocity waveforms were measured most commonly in the clinic. Other methods of clinical measurements have emerged (e.g. ultrasound and magnetic resonance imaging) and wave intensity analysis has been recast in terms of the parameters that are measured. No systematic notation has been developed to distinguish the different variants. This is a possible source of confusion.

1. derivatives vs. differences: Wave intensity is sometime defined as [math]\displaystyle{ \Delta I = \frac{\Delta P}{\Delta t} \frac{\Delta U}{\Delta t} }[/math] which gives results that are independent of the sampling time [math]\displaystyle{ \Delta t }[/math]. This has some advantages but it means that the dimensions of wave intensity are not easily interpreted physically.
2. area (diameter) vs. pressure: High precision pressure measurements are highly invasive and so some researchers measure the instantaneous area (diameter) of the artery instead. By inverting the tube law to [math]\displaystyle{ P = P(A) }[/math], it is possible to eliminate [math]\displaystyle{ P }[/math] from the mass conservation equation. In this formulation [math]\displaystyle{ \Delta I = \Delta ln(A) \Delta U }[/math] ([math]\displaystyle{ = 2 \Delta ln(D) \Delta U }[/math]), which has the dimensions of velocity. This variant retains the advantage that the sign of wave intensity indicates the direction of travel of the dominant wavelets.
3. volume flow rate vs. mean velocity: Sometimes volume flow rate, [math]\displaystyle{ Q = UA }[/math], is most easily measured clinically and wave intensity is defined as [math]\displaystyle{ \Delta I = \Delta P \Delta Q }[/math]. Since the fractional area change is relatively small, this variant of wave intensity behaves very much like the original form. However, in this variant the sign of wave intensity is not always indicative of its direction of travel.

Applications

Although wave intensity has some clinical applications, its main influence has been on the basic understanding of arterial hemodynamics. The first publication pointed out that the deceleration of blood in the aorta during late systole is mainly due to forward deceleration waves rather than backward reflections from the periphery. Backward wavelets are present as indicated by the negative wave intensity during mid-systole but most of the deceleration is caused by forward decompression waves generated when the contraction of the ventricle can not keep up with the flow of blood established by the initial contraction wave.

Various studies have looked at the magnitudes of the forward and backward peaks of wave intensity in various pathologies. In the 1990s, Aloka introduced clinical ultrasound scanners that measured the instantaneous wave intensity directly from simultaneous measurements of diameter (by B-mode) and blood velocity (by Doppler). Recent studies suggest that wave intensity calculated from catheter measurements in the pulmonary artery can be used to differentiate between pulmonary arterial hypertension and chronic thromboembolic pulmonary hypertension.

Wave intensity analysis is frequently used in the study of coronary artery hemodynamics where impedance analysis is seldom, if ever, used. It played an important role in the development of the Instantaneous Wave-free Ratio as a measure of the functional effect of stenoses in the coronary arteries. This method informs an interventional cardiologist if stenting is required by measuring the ratio of downstream and upstream pressures during a period in mid-diastole when the net wave intensity is minimal. Large scale clinical trials have shown that this index is "at least as good as" the Functional Flow Resistance Index which requires the injection of a potent vasodilator.