Medicine:Windkessel effect

Short description: Mechanism that maintains blood pressure between heart beats

The Windkessel analogy illustrated.

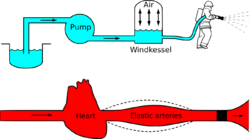
Windkessel effect is a term used in medicine to account for the shape of the arterial blood pressure waveform in terms of the interaction between the stroke volume and the compliance of the aorta and large elastic arteries (Windkessel vessels) and the resistance of the smaller arteries and arterioles. Windkessel when loosely translated from German to English means 'air chamber', but is generally taken to imply an elastic reservoir. The walls of large elastic arteries (e.g. aorta, common carotid, subclavian, and pulmonary arteries and their larger branches) contain elastic fibers, formed of elastin. These arteries distend when the blood pressure rises during systole and recoil when the blood pressure falls during diastole. Since the rate of blood entering these elastic arteries exceeds that leaving them via the peripheral resistance, there is a net storage of blood in the aorta and large arteries during systole, which discharges during diastole. The compliance (or distensibility) of the aorta and large elastic arteries is therefore analogous to a capacitor (employing the hydraulic analogy); to put it another way, these arteries collectively act as a hydraulic accumulator.

The Windkessel effect helps in damping the fluctuation in blood pressure (pulse pressure) over the cardiac cycle and assists in the maintenance of organ perfusion during diastole when cardiac ejection ceases. The idea of the Windkessel was alluded to by Giovanni Borelli, although Stephen Hales articulated the concept more clearly and drew the analogy with an air chamber used in fire engines in the 18th century. Otto Frank, an influential German physiologist, developed the concept and provided a firm mathematical foundation. Frank's model is sometimes called a two-element Windkessel to distinguish it from more recent and more elaborate Windkessel models (e.g. three- or four-element and non-linear Windkessel models).

Model types

Modeling of a Windkessel

Windkessel physiology remains a relevant yet dated description of important clinical interest. The historic mathematical definition of systole and diastole in the model are obviously not novel but are here elementally staged to four degrees. Reaching five would be original work.

Two-element

2-Element Windkessel Circuit Analogy Illustrated

It is assumed that the ratio of pressure to volume is constant and that outflow from the Windkessel is proportional to the fluid pressure. Volumetric inflow must equal the sum of the volume stored in the capacitive element and volumetric outflow through the resistive element. This relationship is described by a differential equation:

[math]\displaystyle{ I(t)={P(t)\over R}+C{dP(t)\over dt} }[/math]

I(t) is volumetric inflow due to the pump (heart) and is measured in volume per unit time, while P(t) is the pressure with respect to time measured in force per unit area, C is the ratio of volume to pressure for the Windkessel, and R is the resistance relating outflow to fluid pressure. This model is identical to the relationship between current, I(t), and electrical potential, P(t), in an electrical circuit equivalent of the two-element Windkessel model.

In the blood circulation, the passive elements in the circuit are assumed to represent elements in the cardiovascular system. The resistor, R, represents the total peripheral resistance and the capacitor, C, represents total arterial compliance.

During diastole there is no blood inflow since the aortic (or pulmonary valve) is closed, so the Windkessel can be solved for P(t) since I(t) = 0:

[math]\displaystyle{ P(t)=P(t_d)e^{-(t-t_d)\over (RC)} }[/math]

where t_d is the time of the start of diastole and P(t_d) is the blood pressure at the start of diastole. This model is only a rough approximation of the arterial circulation; more realistic models incorporate more elements, provide more realistic estimates of the blood pressure waveform and are discussed below.

Three-element

The three-element Windkessel improves on the two-element model by incorporating another resistive element to simulate resistance to blood flow due to the characteristic resistance of the aorta (or pulmonary artery). The differential equation for the 3-element model is:

[math]\displaystyle{ (1+{R_1\over R_2})I(t)+CR_1{dI(t)\over dt}= {P(t)\over R_2}+C{dP(t)\over dt} }[/math]

3-Element

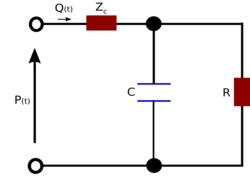
where R₁ is the characteristic resistance (this is assumed to be equivalent to the characteristic impedance), while R₂ represents the peripheral resistance. This model is widely used as an acceptable model of the circulation. For example it has been employed to evaluate blood pressure and flow in the aorta of a chick embryo and the pulmonary artery in a pig as well as providing the basis for construction of physical models of the circulation providing realistic loads for experimental studies of isolated hearts.

Four-element

4-Element compared to the 2- and 3-Element Windkessel models

The three-element model overestimates the compliance and underestimates the characteristic impedance of the circulation. The four-element model includes an inductor, L, which has units of mass per length, ([math]\displaystyle{ {M\over l^4} }[/math]), into the proximal component of the circuit to account for the inertia of blood flow. This is neglected in the two- and three- element models. The relevant equation is:

[math]\displaystyle{ (1+{R_1\over R_2})I(t)+(R_1C+{L\over R_2}){dI(t)\over dt}+LC{d^2I(t)\over dt^2}={P(t)\over R_2}+C{dP(t)\over dt} }[/math]

Applications

These models relate blood flow to blood pressure through parameters of R, C (and, in the case of the four-element model, L). These equations can be easily solved (e.g. by employing MATLAB and its supplement SIMULINK) to either find the values of pressure given flow and R, C, L parameters, or find values of R, C, L given flow and pressure. An example for the two-element model is shown below, where I(t) is depicted as an input signal during systole and diastole. Systole is represented by the sin function, while flow during diastole is zero. s represents the duration of the cardiac cycle, while Ts represents the duration of systole, and Td represents the duration of diastole (e.g. in seconds).

[math]\displaystyle{ I(t)=I_o\sin[{(\pi*{t\over s})\over Ts}] \text{ for } {t\over s}\leq Ts }[/math]

[math]\displaystyle{ I(t)=0\text{ for } Ts\lt (Td+Ts) }[/math]

Graph Evaluating Systole and Diastole Pressure

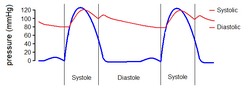
In physiology and disease

The 'Windkessel effect' becomes diminished with age as the elastic arteries become less compliant, termed hardening of the arteries or arteriosclerosis, probably secondary to fragmentation and loss of elastin. The reduction in the Windkessel effect results in increased pulse pressure for a given stroke volume. The increased pulse pressure results in elevated systolic pressure (hypertension) which increases the risk of myocardial infarction, stroke, heart failure and a variety of other cardiovascular diseases.

Limitations

Although the Windkessel is a simple and convenient concept, it has been largely superseded by more modern approaches that interpret arterial pressure and flow waveforms in terms of wave propagation and reflection. Recent attempts to integrate wave propagation and Windkessel approaches through a reservoir concept, have been criticized and a recent consensus document highlighted the wave-like nature of the reservoir.

See also

• Physics:Hydraulic accumulator – Reservoir to store and stabilise fluid pressure