Minimum-cost flow problem

Short description: Mathematical optimization problem

The minimum-cost flow problem (MCFP) is an optimization and decision problem to find the cheapest possible way of sending a certain amount of flow through a flow network. A typical application of this problem involves finding the best delivery route from a factory to a warehouse where the road network has some capacity and cost associated. The minimum cost flow problem is one of the most fundamental among all flow and circulation problems because most other such problems can be cast as a minimum cost flow problem and also that it can be solved efficiently using the network simplex algorithm.

Definition

A flow network is a directed graph [math]\displaystyle{ G=(V,E) }[/math] with a source vertex [math]\displaystyle{ s \in V }[/math] and a sink vertex [math]\displaystyle{ t \in V }[/math], where each edge [math]\displaystyle{ (u,v) \in E }[/math] has capacity [math]\displaystyle{ c(u,v) \gt 0 }[/math], flow [math]\displaystyle{ f(u,v) }[/math] and cost [math]\displaystyle{ a(u,v) }[/math], with most minimum-cost flow algorithms supporting edges with negative costs. The cost of sending this flow along an edge [math]\displaystyle{ (u,v) }[/math] is [math]\displaystyle{ f(u,v)\cdot a(u,v) }[/math]. The problem requires an amount of flow [math]\displaystyle{ d }[/math] to be sent from source [math]\displaystyle{ s }[/math] to sink [math]\displaystyle{ t }[/math].

The definition of the problem is to minimize the total cost of the flow over all edges:

[math]\displaystyle{ \sum_{(u,v) \in E} a(u,v) \cdot f(u,v) }[/math]

with the constraints

Capacity constraints:	[math]\displaystyle{ \,f(u,v) \le c(u,v) }[/math]
Skew symmetry:	[math]\displaystyle{ \,f(u,v) = - f(v,u) }[/math]
Flow conservation:	[math]\displaystyle{ \,\sum_{w \in V} f(u,w) = 0 \text{ for all } u \neq s, t }[/math]
Required flow:	[math]\displaystyle{ \,\sum_{w \in V} f(s,w) = d \text{ and } \sum_{w \in V} f(w,t) = d }[/math]

Relation to other problems

A variation of this problem is to find a flow which is maximum, but has the lowest cost among the maximum flow solutions. This could be called a minimum-cost maximum-flow problem and is useful for finding minimum cost maximum matchings.

With some solutions, finding the minimum cost maximum flow instead is straightforward. If not, one can find the maximum flow by performing a binary search on [math]\displaystyle{ d }[/math].

A related problem is the minimum cost circulation problem, which can be used for solving minimum cost flow. This is achieved by setting the lower bound on all edges to zero, and then making an extra edge from the sink [math]\displaystyle{ t }[/math] to the source [math]\displaystyle{ s }[/math], with capacity [math]\displaystyle{ c(t,s)=d }[/math] and lower bound [math]\displaystyle{ l(t,s)=d }[/math], forcing the total flow from [math]\displaystyle{ s }[/math] to [math]\displaystyle{ t }[/math] to also be [math]\displaystyle{ d }[/math].

The following problems are special cases of the minimum cost flow problem (we provide brief sketches of each applicable reduction, in turn):

• Shortest path problem (single-source). Require that a feasible solution to the minimum cost flow problem sends one unit of flow from a designated source [math]\displaystyle{ s }[/math] to a designated sink [math]\displaystyle{ t }[/math]. Give all edges infinite capacity.
• Maximum flow problem. Let all nodes have zero demand, and let the cost associated with traversing any edge be zero. Now, introduce a new edge [math]\displaystyle{ (t,s) }[/math] from the current sink [math]\displaystyle{ t }[/math] to the current source [math]\displaystyle{ s }[/math]. Stipulate that the per-unit cost of sending flow across edge [math]\displaystyle{ (t,s) }[/math] equals [math]\displaystyle{ -1 }[/math], and permit [math]\displaystyle{ (t,s) }[/math] infinite capacity. (This reduction is also mentioned in Circulation problem).
• Assignment problem. Suppose that each partite set in the bipartition has [math]\displaystyle{ n }[/math] vertices, and denote the bipartition by [math]\displaystyle{ (X,Y) }[/math]. Give each [math]\displaystyle{ x \in X }[/math] supply [math]\displaystyle{ 1/n }[/math] and give each [math]\displaystyle{ y \in Y }[/math] demand [math]\displaystyle{ 1/n }[/math]. Each edge is to have unit capacity.

Solutions

The minimum cost flow problem can be solved by linear programming, since we optimize a linear function, and all constraints are linear.

Apart from that, many combinatorial algorithms exist, for a comprehensive survey, see . Some of them are generalizations of maximum flow algorithms, others use entirely different approaches.

Well-known fundamental algorithms (they have many variations):

• Cycle canceling: a general primal method.
• Cut canceling: a general dual method.
• Minimum mean cycle canceling: a simple strongly polynomial algorithm.
• Successive shortest path and capacity scaling: dual methods, which can be viewed as the generalization of the Ford–Fulkerson algorithm.
• Cost scaling: a primal-dual approach, which can be viewed as the generalization of the push-relabel algorithm.
• Network simplex algorithm: a specialized version of the linear programming simplex method.
• Out-of-kilter algorithm by D. R. Fulkerson

Application

Minimum weight bipartite matching

Reducing Minimum weight bipartite matching to minimum cost max flow problem

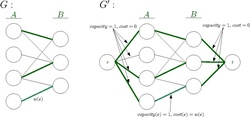
Given a bipartite graph G = (A ∪ B, E), the goal is to find the maximum cardinality matching in G that has minimum cost. Let w: E → R be a weight function on the edges of E. The minimum weight bipartite matching problem or assignment problem is to find a perfect matching M ⊆ E whose total weight is minimized. The idea is to reduce this problem to a network flow problem.

Let G′ = (V′ = A ∪ B, E′ = E). Assign the capacity of all the edges in E′ to 1. Add a source vertex s and connect it to all the vertices in A′ and add a sink vertex t and connect all vertices inside group B′ to this vertex. The capacity of all the new edges is 1 and their costs is 0. It is proved that there is minimum weight perfect bipartite matching in G if and only if there a minimum cost flow in G′.

See also

• LEMON (C++ library)
• GNU Linear Programming Kit
• Network flow problem

References

1. ^ Ravindra K. Ahuja; Thomas L. Magnanti; James B. Orlin (1993). Network Flows: Theory, Algorithms, and Applications. Prentice-Hall, Inc.. ISBN 978-0-13-617549-0. 
2. ^ Morton Klein (1967). "A primal method for minimal cost flows with applications to the assignment and transportation problems". Management Science 14 (3): 205–220. doi:10.1287/mnsc.14.3.205. 
3. ^ Refael Hassin (1983). "The minimum cost flow problem: A unifying approach to existing algorithms and a new tree search algorithm". Mathematical Programming 25: 228-239. doi:10.1007/bf02591772. 
4. ^ Thomas R. Ervolina & S. Thomas McCormick (1993). "Two strongly polynomial cut cancelling algorithms for minimum cost network flow". Discrete Applied Mathematics 4: 133-165. doi:10.1016/0166-218x(93)90025-j. 
5. ^ Andrew V. Goldberg; Robert E. Tarjan (1989). "Finding minimum-cost circulations by canceling negative cycles". Journal of the ACM 36 (4): 873–886. doi:10.1145/76359.76368. 
6. ^ Jack Edmonds; Richard M. Karp (1972). "Theoretical improvements in algorithmic efficiency for network flow problems". Journal of the ACM 19 (2): 248–264. doi:10.1145/321694.321699. 
7. ^ "Finding minimum-cost circulations by successive approximation". Mathematics of Operations Research 15 (3): 430–466. 1990. doi:10.1287/moor.15.3.430. 
8. ^ James B. Orlin (1997). "A polynomial time primal network simplex algorithm for minimum cost flows". Mathematical Programming 78 (2): 109–129. doi:10.1007/bf02614365. 

External links

• LEMON C++ library with several maximum flow and minimum cost circulation algorithms
• The MCFClass C++ project library with some minimum cost flow and shortest path algorithms