Ford–Fulkerson algorithm
The Ford–Fulkerson method or Ford–Fulkerson algorithm (FFA) is a greedy algorithm that computes the maximum flow in a flow network. It is sometimes called a "method" instead of an "algorithm" as the approach to finding augmenting paths in a residual graph is not fully specified[1] or it is specified in several implementations with different running times.[2] It was published in 1956 by L. R. Ford Jr. and D. R. Fulkerson.[3] The name "Ford–Fulkerson" is often also used for the Edmonds–Karp algorithm, which is a fully defined implementation of the Ford–Fulkerson method.
The idea behind the algorithm is as follows: as long as there is a path from the source (start node) to the sink (end node), with available capacity on all edges in the path, we send flow along one of the paths. Then we find another path, and so on. A path with available capacity is called an augmenting path.
Algorithm
Let be a graph, and for each edge from u to v, let be the capacity and be the flow. We want to find the maximum flow from the source s to the sink t. After every step in the algorithm the following is maintained:
Capacity constraints The flow along an edge cannot exceed its capacity. Skew symmetry The net flow from u to v must be the opposite of the net flow from v to u (see example). Flow conservation The net flow to a node is zero, except for the source, which "produces" flow, and the sink, which "consumes" flow. Value(f) The flow leaving from s must be equal to the flow arriving at t.
This means that the flow through the network is a legal flow after each round in the algorithm. We define the residual network to be the network with capacity and no flow. Notice that it can happen that a flow from v to u is allowed in the residual network, though disallowed in the original network: if and then .
Algorithm Ford–Fulkerson
- Inputs Given a Network with flow capacity c, a source node s, and a sink node t
- Output Compute a flow f from s to t of maximum value
- for all edges
- While there is a path p from s to t in , such that for all edges :
- Find
- For each edge
- (Send flow along the path)
- (The flow might be "returned" later)
- "←" denotes assignment. For instance, "largest ← item" means that the value of largest changes to the value of item.
- "return" terminates the algorithm and outputs the following value.
The path in step 2 can be found with, for example, a breadth-first search (BFS) or a depth-first search in . If you use the former, the algorithm is called Edmonds–Karp.
When no more paths in step 2 can be found, s will not be able to reach t in the residual network. If S is the set of nodes reachable by s in the residual network, then the total capacity in the original network of edges from S to the remainder of V is on the one hand equal to the total flow we found from s to t, and on the other hand serves as an upper bound for all such flows. This proves that the flow we found is maximal. See also Max-flow Min-cut theorem.
If the graph has multiple sources and sinks, we act as follows: Suppose that and . Add a new source with an edge from to every node , with capacity . And add a new sink with an edge from every node to , with capacity . Then apply the Ford–Fulkerson algorithm.
Also, if a node u has capacity constraint , we replace this node with two nodes , and an edge , with capacity . Then apply the Ford–Fulkerson algorithm.
Complexity
By adding the flow augmenting path to the flow already established in the graph, the maximum flow will be reached when no more flow augmenting paths can be found in the graph. However, there is no certainty that this situation will ever be reached, so the best that can be guaranteed is that the answer will be correct if the algorithm terminates. In the case that the algorithm runs forever, the flow might not even converge towards the maximum flow. However, this situation only occurs with irrational flow values.[4] When the capacities are integers, the runtime of Ford–Fulkerson is bounded by (see big O notation), where is the number of edges in the graph and is the maximum flow in the graph. This is because each augmenting path can be found in time and increases the flow by an integer amount of at least , with the upper bound .
A variation of the Ford–Fulkerson algorithm with guaranteed termination and a runtime independent of the maximum flow value is the Edmonds–Karp algorithm, which runs in time.
Integral example
The following example shows the first steps of Ford–Fulkerson in a flow network with 4 nodes, source and sink . This example shows the worst-case behaviour of the algorithm. In each step, only a flow of is sent across the network. If breadth-first-search were used instead, only two steps would be needed.
| Path | Capacity | Resulting flow network |
|---|---|---|
| Initial flow network | 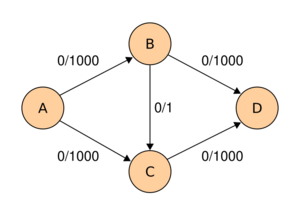
| |
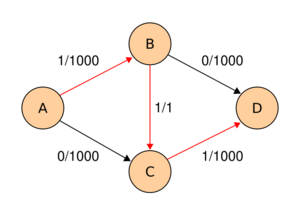
| ||
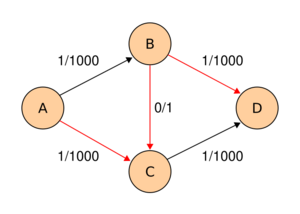
| ||
| After 1998 more steps ... | ||
| Final flow network | 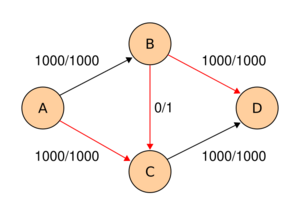
| |
Notice how flow is "pushed back" from to when finding the path .
Non-terminating example

Consider the flow network shown on the right, with source , sink , capacities of edges , and respectively , and and the capacity of all other edges some integer . The constant was chosen so, that . We use augmenting paths according to the following table, where , and .
| Step | Augmenting path | Sent flow | Residual capacities | ||
|---|---|---|---|---|---|
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
Note that after step 1 as well as after step 5, the residual capacities of edges , and are in the form , and , respectively, for some . This means that we can use augmenting paths , , and infinitely many times and residual capacities of these edges will always be in the same form. Total flow in the network after step 5 is . If we continue to use augmenting paths as above, the total flow converges to . However, note that there is a flow of value , by sending units of flow along , 1 unit of flow along , and units of flow along . Therefore, the algorithm never terminates and the flow does not even converge to the maximum flow.[5]
Another non-terminating example based on the Euclidean algorithm is given by (Backman Huynh), where they also show that the worst case running-time of the Ford-Fulkerson algorithm on a network in ordinal numbers is .
Python implementation of Edmonds–Karp algorithm
import collections
class Graph:
"""
This class represents a directed graph using
adjacency matrix representation.
"""
def __init__(self, graph):
self.graph = graph # residual graph
self.row = len(graph)
def bfs(self, s, t, parent):
"""
Returns true if there is a path from
source 's' to sink 't' in residual graph.
Also fills parent[] to store the path.
"""
# Mark all the vertices as not visited
visited = [False] * self.row
# Create a queue for BFS
queue = collections.deque()
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
# Standard BFS loop
while queue:
u = queue.popleft()
# Get all adjacent vertices of the dequeued vertex u
# If an adjacent has not been visited, then mark it
# visited and enqueue it
for ind, val in enumerate(self.graph[u]):
if (visited[ind] == False) and (val > 0):
queue.append(ind)
visited[ind] = True
parent[ind] = u
# If we reached sink in BFS starting from source, then return
# true, else false
return visited[t]
# Returns the maximum flow from s to t in the given graph
def edmonds_karp(self, source, sink):
# This array is filled by BFS and to store path
parent = [-1] * self.row
max_flow = 0 # There is no flow initially
# Augment the flow while there is path from source to sink
while self.bfs(source, sink, parent):
# Find minimum residual capacity of the edges along the
# path filled by BFS. Or we can say find the maximum flow
# through the path found.
path_flow = float("Inf")
s = sink
while s != source:
path_flow = min(path_flow, self.graph[parent[s]][s])
s = parent[s]
# Add path flow to overall flow
max_flow += path_flow
# update residual capacities of the edges and reverse edges
# along the path
v = sink
while v != source:
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
See also
Notes
- ↑ Laung-Terng Wang, Yao-Wen Chang, Kwang-Ting (Tim) Cheng (2009). Electronic Design Automation: Synthesis, Verification, and Test. Morgan Kaufmann. pp. 204. ISBN 978-0080922003. https://archive.org/details/electronicdesign00wang.
- ↑ Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein (2009). Introduction to Algorithms. MIT Press. pp. 714. ISBN 978-0262258104. https://archive.org/details/introductiontoal00corm_805.
- ↑ Ford, L. R.; Fulkerson, D. R. (1956). "Maximal flow through a network". Canadian Journal of Mathematics 8: 399–404. doi:10.4153/CJM-1956-045-5. http://www.cs.yale.edu/homes/lans/readings/routing/ford-max_flow-1956.pdf.
- ↑ "Ford-Fulkerson Max Flow Labeling Algorithm". 1998. CiteSeerX 10.1.1.295.9049.
- ↑ Zwick, Uri (21 August 1995). "The smallest networks on which the Ford–Fulkerson maximum flow procedure may fail to terminate". Theoretical Computer Science 148 (1): 165–170. doi:10.1016/0304-3975(95)00022-O.
References
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Section 26.2: The Ford–Fulkerson method". Introduction to Algorithms (Second ed.). MIT Press and McGraw–Hill. pp. 651–664. ISBN 0-262-03293-7.
- George T. Heineman; Gary Pollice; Stanley Selkow (2008). "Chapter 8:Network Flow Algorithms". Algorithms in a Nutshell. Oreilly Media. pp. 226–250. ISBN 978-0-596-51624-6.
- Jon Kleinberg; Éva Tardos (2006). "Chapter 7:Extensions to the Maximum-Flow Problem". Algorithm Design. Pearson Education. pp. 378–384. ISBN 0-321-29535-8. https://archive.org/details/algorithmdesign0000klei/page/378.
- Samuel Gutekunst (2019). ENGRI 1101. Cornell University.
- Backman, Spencer; Huynh, Tony (2018). "Transfinite Ford–Fulkerson on a finite network". Computability 7 (4): 341–347. doi:10.3233/COM-180082.
External links
- A tutorial explaining the Ford–Fulkerson method to solve the max-flow problem
- Another Java animation
- Java Web Start application
 |
