Morse theory
In mathematics, specifically in differential topology, Morse theory enables one to analyze the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a typical differentiable function on a manifold will reflect the topology quite directly. Morse theory allows one to find CW structures and handle decompositions on manifolds and to obtain substantial information about their homology.
Before Morse, Arthur Cayley and James Clerk Maxwell had developed some of the ideas of Morse theory in the context of topography. Morse originally applied his theory to geodesics (critical points of the energy functional on the space of paths). These techniques were used in Raoul Bott's proof of his periodicity theorem.
The analogue of Morse theory for complex manifolds is Picard–Lefschetz theory.
Basic concepts
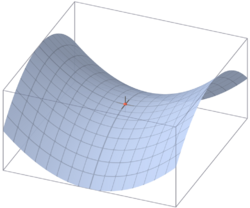
To illustrate, consider a mountainous landscape surface (more generally, a manifold). If is the function giving the elevation of each point, then the inverse image of a point in is a contour line (more generally, a level set). Each connected component of a contour line is either a point, a simple closed curve, or a closed curve with a double point. Contour lines may also have points of higher order (triple points, etc.), but these are unstable and may be removed by a slight deformation of the landscape. Double points in contour lines occur at saddle points, or passes, where the surrounding landscape curves up in one direction and down in the other.
Imagine flooding this landscape with water. When the water reaches elevation , the underwater surface is , the points with elevation or below. Consider how the topology of this surface changes as the water rises. It appears unchanged except when passes the height of a critical point, where the gradient of is (more generally, the Jacobian matrix acting as a linear map between tangent spaces does not have maximal rank). In other words, the topology of does not change except when the water either (1) starts filling a basin, (2) covers a saddle (a mountain pass), or (3) submerges a peak.

To these three types of critical points—basins, passes, and peaks (i.e. minima, saddles, and maxima)—one associates a number called the index, the number of independent directions in which decreases from the point. More precisely, the index of a non-degenerate critical point of is the dimension of the largest subspace of the tangent space to at on which the Hessian of is negative definite. The indices of basins, passes, and peaks are and respectively.
Considering a more general surface, let be a torus oriented as in the picture, with again taking a point to its height above the plane. One can again analyze how the topology of the underwater surface changes as the water level rises.

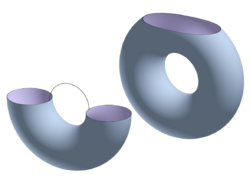
Starting from the bottom of the torus, let and be the four critical points of index and corresponding to the basin, two saddles, and peak, respectively. When is less than then is the empty set. After passes the level of when then is a disk, which is homotopy equivalent to a point (a 0-cell) which has been "attached" to the empty set. Next, when exceeds the level of and then is a cylinder, and is homotopy equivalent to a disk with a 1-cell attached (image at left). Once passes the level of and then is a torus with a disk removed, which is homotopy equivalent to a cylinder with a 1-cell attached (image at right). Finally, when is greater than the critical level of is a torus, i.e. a torus with a disk (a 2-cell) removed and re-attached.
This illustrates the following rule: the topology of does not change except when passes the height of a critical point; at this point, a -cell is attached to , where is the index of the point. This does not address what happens when two critical points are at the same height, which can be resolved by a slight perturbation of In the case of a landscape or a manifold embedded in Euclidean space, this perturbation might simply be tilting slightly, rotating the coordinate system.
One must take care to make the critical points non-degenerate. To see what can pose a problem, let and let Then is a critical point of but the topology of does not change when passes The problem is that the second derivative is —that is, the Hessian of vanishes and the critical point is degenerate. This situation is unstable, since by slightly deforming to , the degenerate critical point is either removed () or breaks up into two non-degenerate critical points ().
Formal development
For a real-valued smooth function on a differentiable manifold the points where the differential of vanishes are called critical points of and their images under are called critical values. If at a critical point the matrix of second partial derivatives (the Hessian matrix) is non-singular, then is called a non-degenerate critical point; if the Hessian is singular then is a degenerate critical point.
For the functions from to has a critical point at the origin if which is non-degenerate if (that is, is of the form ) and degenerate if (that is, is of the form ). A less trivial example of a degenerate critical point is the origin of the monkey saddle.
The index of a non-degenerate critical point of is the dimension of the largest subspace of the tangent space to at on which the Hessian is negative definite. This corresponds to the intuitive notion that the index is the number of directions in which decreases. The degeneracy and index of a critical point are independent of the choice of the local coordinate system used, as shown by Sylvester's Law.
Morse lemma
Let be a non-degenerate critical point of Then there exists a chart in a neighborhood of such that for all and throughout Here is equal to the index of at . As a corollary of the Morse lemma, one sees that non-degenerate critical points are isolated. (Regarding an extension to the complex domain see Complex Morse Lemma. For a generalization, see Morse–Palais lemma).
Fundamental theorems
A smooth real-valued function on a manifold is a Morse function if it has no degenerate critical points. A basic result of Morse theory says that almost all functions are Morse functions. Technically, the Morse functions form an open, dense subset of all smooth functions in the topology. This is sometimes expressed as "a typical function is Morse" or "a generic function is Morse".
As indicated before, we are interested in the question of when the topology of changes as varies. Half of the answer to this question is given by the following theorem.
- Theorem. Suppose is a smooth real-valued function on is compact, and there are no critical values between and Then is diffeomorphic to and deformation retracts onto
It is also of interest to know how the topology of changes when passes a critical point. The following theorem answers that question.
- Theorem. Suppose is a smooth real-valued function on and is a non-degenerate critical point of of index and that Suppose is compact and contains no critical points besides Then is homotopy equivalent to with a -cell attached.
These results generalize and formalize the 'rule' stated in the previous section.
Using the two previous results and the fact that there exists a Morse function on any differentiable manifold, one can prove that any differentiable manifold is a CW complex with an -cell for each critical point of index To do this, one needs the technical fact that one can arrange to have a single critical point on each critical level, which is usually proven by using gradient-like vector fields to rearrange the critical points.
Morse inequalities
Morse theory can be used to prove some strong results on the homology of manifolds. The number of critical points of index of is equal to the number of cells in the CW structure on obtained from "climbing" Using the fact that the alternating sum of the ranks of the homology groups of a topological space is equal to the alternating sum of the ranks of the chain groups from which the homology is computed, then by using the cellular chain groups (see cellular homology) it is clear that the Euler characteristic is equal to the sum where is the number of critical points of index Also by cellular homology, the rank of the th homology group of a CW complex is less than or equal to the number of -cells in Therefore, the rank of the th homology group, that is, the Betti number , is less than or equal to the number of critical points of index of a Morse function on These facts can be strengthened to obtain the Morse inequalities:
In particular, for any one has
This gives a powerful tool to study manifold topology. Suppose on a closed manifold there exists a Morse function with precisely k critical points. In what way does the existence of the function restrict ? The case was studied by Georges Reeb in 1952; the Reeb sphere theorem states that is homeomorphic to a sphere The case is possible only in a small number of low dimensions, and M is homeomorphic to an Eells–Kuiper manifold. In 1982 Edward Witten developed an analytic approach to the Morse inequalities by considering the de Rham complex for the perturbed operator [1][2]
Application to classification of closed 2-manifolds
Morse theory has been used to classify closed 2-manifolds up to diffeomorphism. If is oriented, then is classified by its genus and is diffeomorphic to a sphere with handles: thus if is diffeomorphic to the 2-sphere; and if is diffeomorphic to the connected sum of 2-tori. If is unorientable, it is classified by a number and is diffeomorphic to the connected sum of real projective spaces In particular two closed 2-manifolds are homeomorphic if and only if they are diffeomorphic.[3][4][5]
Morse homology
Morse homology is a particularly easy way to understand the homology of smooth manifolds. It is defined using a generic choice of Morse function and Riemannian metric. The basic theorem is that the resulting homology is an invariant of the manifold (that is, independent of the function and metric) and isomorphic to the singular homology of the manifold; this implies that the Morse and singular Betti numbers agree and gives an immediate proof of the Morse inequalities. An infinite dimensional analog of Morse homology in symplectic geometry is known as Floer homology.
Morse–Bott theory
The notion of a Morse function can be generalized to consider functions that have nondegenerate manifolds of critical points. A Morse–Bott function is a smooth function on a manifold whose critical set is a closed submanifold and whose Hessian is non-degenerate in the normal direction. (Equivalently, the kernel of the Hessian at a critical point equals the tangent space to the critical submanifold.) A Morse function is the special case where the critical manifolds are zero-dimensional (so the Hessian at critical points is non-degenerate in every direction, that is, has no kernel).
The index is most naturally thought of as a pair where is the dimension of the unstable manifold at a given point of the critical manifold, and is equal to plus the dimension of the critical manifold. If the Morse–Bott function is perturbed by a small function on the critical locus, the index of all critical points of the perturbed function on a critical manifold of the unperturbed function will lie between and
Morse–Bott functions are useful because generic Morse functions are difficult to work with; the functions one can visualize, and with which one can easily calculate, typically have symmetries. They often lead to positive-dimensional critical manifolds. Raoul Bott used Morse–Bott theory in his original proof of the Bott periodicity theorem.
Round functions are examples of Morse–Bott functions, where the critical sets are (disjoint unions of) circles.
Morse homology can also be formulated for Morse–Bott functions; the differential in Morse–Bott homology is computed by a spectral sequence. Frederic Bourgeois sketched an approach in the course of his work on a Morse–Bott version of symplectic field theory, but this work was never published due to substantial analytic difficulties.
See also
References
- ↑ Witten, Edward (1982). "Supersymmetry and Morse theory". J. Differential Geom. 17 (4): 661–692. doi:10.4310/jdg/1214437492.
- ↑ Roe, John (1998). Elliptic Operators, Topology and Asymptotic Method. Pitman Research Notes in Mathematics Series. 395 (2nd ed.). Longman. ISBN 0582325021.
- ↑ Smale 1994[full citation needed]
- ↑ Gauld, David B. (1982). Differential Topology: an Introduction. Monographs and Textbooks in Pure and Applied Mathematics. 72. Marcel Dekker. ISBN 0824717090. https://archive.org/details/differentialtopo0000gaul.
- ↑ Shastri, Anant R. (2011). Elements of Differential Topology. CRC Press. ISBN 9781439831601. https://books.google.com/books?id=-BrOBQAAQBAJ.
Further reading
- Bott, Raoul (1988). "Morse Theory Indomitable". Publications Mathématiques de l'IHÉS 68: 99–114. doi:10.1007/bf02698544. http://www.numdam.org/item?id=PMIHES_1988__68__99_0.
- Bott, Raoul (1982). "Lectures on Morse theory, old and new". Bulletin of the American Mathematical Society. (N.S.) 7 (2): 331–358. doi:10.1090/s0273-0979-1982-15038-8.
- Cayley, Arthur (1859). "On Contour and Slope Lines". The Philosophical Magazine 18 (120): 264–268. http://www.maths.ed.ac.uk/~aar/papers/cayleyconslo.pdf.
- Guest, Martin (2001). "Morse Theory in the 1990s". arXiv:math/0104155.
- Hirsch, M. (1994). Differential Topology (2nd ed.). Springer.
- Template:Kosinski Differential Manifolds 2007
- Template:Lang Fundamentals of Differential Geometry
- Matsumoto, Yukio (2002). An Introduction to Morse Theory.
- Maxwell, James Clerk (1870). "On Hills and Dales". The Philosophical Magazine 40 (269): 421–427. https://www.maths.ed.ac.uk/~v1ranick/surgery/hilldale.pdf.
- Milnor, John (1963). Morse Theory. Princeton University Press. ISBN 0-691-08008-9. A classic advanced reference in mathematics and mathematical physics.
- Milnor, John (1965). Lectures on the h-cobordism theorem. https://www.maths.ed.ac.uk/~v1ranick/surgery/hcobord.pdf.
- Morse, Marston (1934). The Calculus of Variations in the Large. American Mathematical Society Colloquium Publication. 18. New York.
- Schwarz, Matthias (1993). Morse Homology. Birkhäuser. ISBN 9780817629045. https://archive.org/details/morsehomology0000schw.
 |
