Multiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system.
The decimal multiplication table was traditionally taught as an essential part of elementary arithmetic around the world, as it lays the foundation for arithmetic operations with base-ten numbers. Many educators believe it is necessary to memorize the table up to 9 × 9.[1]
History
Pre-modern times

The oldest known multiplication tables were used by the Babylonians about 4000 years ago.[2] However, they used a base of 60.[2] The oldest known tables using a base of 10 are the Chinese decimal multiplication table on bamboo strips dating to about 305 BC, during China's Warring States period.[2]
The multiplication table is sometimes attributed to the ancient Greek mathematician Pythagoras (570–495 BC). It is also called the Table of Pythagoras in many languages (for example French, Italian and Russian), sometimes in English.[4] The Greco-Roman mathematician Nichomachus (60–120 AD), a follower of Neopythagoreanism, included a multiplication table in his Introduction to Arithmetic, whereas the oldest surviving Greek multiplication table is on a wax tablet dated to the 1st century AD and currently housed in the British Museum.[5]
In 493 AD, Victorius of Aquitaine wrote a 98-column multiplication table which gave (in Roman numerals) the product of every number from 2 to 50 times and the rows were "a list of numbers starting with one thousand, descending by hundreds to one hundred, then descending by tens to ten, then by ones to one, and then the fractions down to 1/144."[6]
Modern times
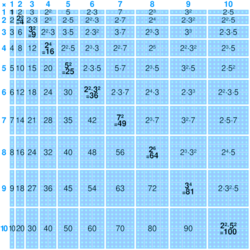
In his 1820 book The Philosophy of Arithmetic,[7] mathematician John Leslie published a multiplication table up to 99 × 99, which allows numbers to be multiplied in pairs of digits at a time. Leslie also recommended that young pupils memorize the multiplication table up to 50 × 50.
The illustration below shows a table up to 12 × 12, which is a size commonly used nowadays in English-world schools.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 11 | 0 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 |
| 12 | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
Because multiplication of integers is commutative, many schools use a smaller table as below. Some schools even remove the first column since 1 is the multiplicative identity.
| 1 | 1 | ||||||||
| 2 | 2 | 4 | |||||||
| 3 | 3 | 6 | 9 | ||||||
| 4 | 4 | 8 | 12 | 16 | |||||
| 5 | 5 | 10 | 15 | 20 | 25 | ||||
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | |||
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | ||
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
The traditional rote learning of multiplication was based on memorization of columns in the table, in a form like
1 × 10 = 10
2 × 10 = 20
3 × 10 = 30
4 × 10 = 40
5 × 10 = 50
6 × 10 = 60
7 × 10 = 70
8 × 10 = 80
9 × 10 = 90
This form of writing the multiplication table in columns with complete number sentences is still used in some countries, such as Bosnia and Herzegovina,[citation needed] instead of the modern grids above.
Patterns in the tables
There is a pattern in the multiplication table that can help people to memorize the table more easily. It uses the figures below:
| → | → | |||||||||
| ↑ | 1 | 2 | 3 | ↓ | ↑ | 2 | 4 | ↓ | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 5 | 6 | ||||||||
| 7 | 8 | 9 | 6 | 8 | ||||||
| ← | ← | |||||||||
| 0 | 5 | 0 | ||||||||
| Figure 1: Odd | Figure 2: Even | |||||||||

Figure 1 is used for multiples of 1, 3, 7, and 9. Figure 2 is used for the multiples of 2, 4, 6, and 8. These patterns can be used to memorize the multiples of any number from 0 to 10, except 5. As you would start on the number you are multiplying, when you multiply by 0, you stay on 0 (0 is external and so the arrows have no effect on 0, otherwise 0 is used as a link to create a perpetual cycle). The pattern also works with multiples of 10, by starting at 1 and simply adding 0, giving you 10, then just apply every number in the pattern to the "tens" unit as you would normally do as usual to the "ones" unit.
For example, to recall all the multiples of 7:
- Look at the 7 in the first picture and follow the arrow.
- The next number in the direction of the arrow is 4. So think of the next number after 7 that ends with 4, which is 14.
- The next number in the direction of the arrow is 1. So think of the next number after 14 that ends with 1, which is 21.
- After coming to the top of this column, start with the bottom of the next column, and travel in the same direction. The number is 8. So think of the next number after 21 that ends with 8, which is 28.
- Proceed in the same way until the last number, 3, corresponding to 63.
- Next, use the 0 at the bottom. It corresponds to 70.
- Then, start again with the 7. This time it will correspond to 77.
- Continue like this.
In abstract algebra
Tables can also define binary operations on groups, fields, rings, and other algebraic systems. In such contexts they are called Cayley tables. Here are the addition and multiplication tables for the finite field Z5:
- for every natural number n, there are also addition and multiplication tables for the ring Zn.
|
|
For other examples, see group, and octonion.
Chinese and Japanese multiplication tables
Mokkan discovered at Heijō Palace suggest that the multiplication table may have been introduced to Japan through Chinese mathematical treatises such as the Sunzi Suanjing, because their expression of the multiplication table share the character 如 in products less than ten.[8] Chinese and Japanese share a similar system of eighty-one short, easily memorable sentences taught to students to help them learn the multiplication table up to 9 × 9. In current usage, the sentences that express products less than ten include an additional particle in both languages. In the case of modern Chinese, this is 得 (dé); and in Japanese, this is が (ga). This is useful for those who practice calculation with a suanpan or a soroban, because the sentences remind them to shift one column to the right when inputting a product that does not begin with a tens digit. In particular, the Japanese multiplication table uses non-standard pronunciations for numbers in some specific instances (such as the replacement of san roku with saburoku).
| × | 1 ichi | 2 ni | 3 san | 4 shi | 5 go | 6 roku | 7 shichi | 8 ha | 9 ku |
|---|---|---|---|---|---|---|---|---|---|
| 1 in | in'ichi ga ichi | inni ga ni | insan ga san | inshi ga shi | ingo ga go | inroku ga roku | inshichi ga shichi | inhachi ga hachi | inku ga ku |
| 2 ni | ni ichi ga ni | ni nin ga shi | ni san ga roku | ni shi ga hachi | ni go jū | ni roku jūni | ni shichi jūshi | ni hachi jūroku | ni ku jūhachi |
| 3 san | san ichi ga san | san ni ga roku | sazan ga ku | san shi jūni | san go jūgo | saburoku jūhachi | san shichi nijūichi | sanpa nijūshi | san ku nijūshichi |
| 4 shi | shi ichi ga shi | shi ni ga hachi | shi san jūni | shi shi jūroku | shi go nijū | shi roku nijūshi | shi shichi nijūhachi | shi ha sanjūni | shi ku sanjūroku |
| 5 go | go ichi ga go | go ni jū | go san jūgo | go shi nijū | go go nijūgo | go roku sanjū | go shichi sanjūgo | go ha shijū | gokku shijūgo |
| 6 roku | roku ichi ga roku | roku ni nijū | roku san jūhachi | roku shi nijūshi | roku go sanjū | roku roku sanjūroku | roku shichi shijūni | roku ha shijūhachi | rokku gojūshi |
| 7 shichi | shichi ichi ga shichi | shichi ni jūshi | shichi san nijūichi | shichi shi nijūhachi | shichi go sanjūgo | shichi roku shijūni | shichi shichi shijūku | shichi ha gojūroku | shichi ku rokujūsan |
| 8 hachi | hachi ichi ga hachi | hachi ni jūroku | hachi san nijūshi | hachi shi sanjūni | hachi go shijū | hachi roku shijūhachi | hachi shichi gojūroku | happa rokujūshi | hakku shichijūni |
| 9 ku | ku ichi ga ku | ku ni jūhachi | ku san nijūshichi | ku shi sanjūroku | ku go shijūgo | ku roku gojūshi | ku shichi rokujūsan | ku ha shichijūni | ku ku hachijūichi |
Warring States decimal multiplication bamboo slips
A bundle of 21 bamboo slips dated 305 BC in the Warring States period in the Tsinghua Bamboo Slips (清華簡) collection is the world's earliest known example of a decimal multiplication table.[9]
Standards-based mathematics reform in the US
In 1989, the National Council of Teachers of Mathematics (NCTM) developed new standards which were based on the belief that all students should learn higher-order thinking skills, which recommended reduced emphasis on the teaching of traditional methods that relied on rote memorization, such as multiplication tables. Widely adopted texts such as Investigations in Numbers, Data, and Space (widely known as TERC after its producer, Technical Education Research Centers) omitted aids such as multiplication tables in early editions. NCTM made it clear in their 2006 Focal Points that basic mathematics facts must be learned, though there is no consensus on whether rote memorization is the best method. In recent years, a number of nontraditional methods have been devised to help children learn multiplication facts, including video-game style apps and books that aim to teach times tables through character-based stories.
See also
- Vedic square
- IBM 1620, an early computer that used tables stored in memory to perform addition and multiplication
References
 |
- ↑ Trivett, John (1980), "The Multiplication Table: To Be Memorized or Mastered!", For the Learning of Mathematics 1 (1): 21–25.
- ↑ Jump up to: 2.0 2.1 2.2 Qiu, Jane (January 7, 2014). "Ancient times table hidden in Chinese bamboo strips". Nature News. doi:10.1038/nature.2014.14482. http://www.nature.com/news/ancient-times-table-hidden-in-chinese-bamboo-strips-1.14482.
- ↑ Wikisource:Page:Popular Science Monthly Volume 26.djvu/467
- ↑ for example in An Elementary Treatise on Arithmetic by John Farrar
- ↑ David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics. New York: Dover Publications (a reprint of the 1951 publication), ISBN 0-486-20429-4, pp. 58, 129.
- ↑ David W. Maher and John F. Makowski. "Literary evidence for Roman arithmetic with fractions". Classical Philology, 96/4 (October 2001), p. 383.
- ↑ Leslie, John (1820). The Philosophy of Arithmetic; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand. Edinburgh: Abernethy & Walker.
- ↑ "「九九」は中国伝来…平城宮跡から木簡出土". Yomiuri Shimbun. December 4, 2010. https://www.yomiuri.co.jp/kyoiku/news/20101204-OYT8T00242.htm.
- ↑ Nature article The 2,300-year-old matrix is the world's oldest decimal multiplication table