Negative frequency
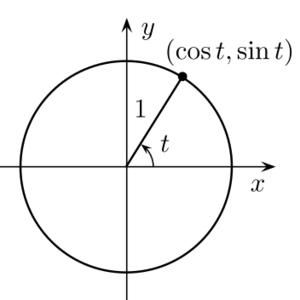
In mathematics, the concept of signed frequency (negative and positive frequency) can indicate both the rate and sense of rotation; it can be as simple as a wheel rotating clockwise or counterclockwise. The rate is expressed in units such as revolutions (a.k.a. cycles) per second (hertz) or radian/second (where 1 cycle corresponds to 2π radians).
Example: Mathematically speaking, the vector [math]\displaystyle{ (\cos(t), \sin(t)) }[/math] has a positive frequency of +1 radian per unit of time and rotates counterclockwise around the unit circle, while the vector [math]\displaystyle{ (\cos(-t), \sin(-t)) }[/math] has a negative frequency of -1 radian per unit of time, which rotates clockwise instead.
Sinusoids
Let ω > 0 be an angular frequency with units of radians/second. Then the function f(t) = −ωt + θ has slope −ω, which is called a negative frequency. But when the function is used as the argument of a cosine operator, the result is indistinguishable from cos(ωt − θ). Similarly, sin(−ωt + θ) is indistinguishable from sin(ωt − θ + π). Thus any sinusoid can be represented in terms of a positive frequency. The sign of the underlying phase slope is ambiguous.
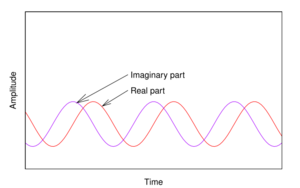
The ambiguity is resolved when the cosine and sine operators can be observed simultaneously, because cos(ωt + θ) leads sin(ωt + θ) by 1⁄4 cycle (i.e. π⁄2 radians) when ω > 0, and lags by 1⁄4 cycle when ω < 0. Similarly, a vector, (cos ωt, sin ωt), rotates counter-clockwise if ω > 0, and clockwise if ω < 0. Therefore, the sign of [math]\displaystyle{ \omega }[/math] is also preserved in the complex-valued function:
[math]\displaystyle{ e^{i \omega t} = \underbrace{\cos(\omega t)}_{R(t)} + i \cdot \underbrace{\sin(\omega t)}_{I(t)}, }[/math] |
|
( ) |
whose corollary is:
[math]\displaystyle{ \cos(\omega t) = \begin{matrix}\frac{1}{2}\end{matrix}\left(e^{i \omega t} + e^{-i \omega t}\right). }[/math] |
|
( ) |
In Eq.1 the second term is an addition to [math]\displaystyle{ \cos(\omega t) }[/math] that resolves the ambiguity. In Eq.2 the second term looks like an addition, but it is actually a cancellation that reduces a 2-dimensional vector to just one dimension, resulting in the ambiguity. Eq.2 also shows why the Fourier transform has responses at both [math]\displaystyle{ \pm \omega, }[/math] even though [math]\displaystyle{ \omega }[/math] can have only one sign. What the false response does is enable the inverse transform to distinguish between a real-valued function and a complex one.
Applications
Simplifying the Fourier transform
Perhaps the best-known application of negative frequency is the formula:
- [math]\displaystyle{ \hat{f}(\omega) = \int_{-\infty}^\infty f(t) e^{-i \omega t} dt, }[/math]
which is a measure of the energy in function [math]\displaystyle{ f(t) }[/math] at frequency [math]\displaystyle{ \omega. }[/math] When evaluated for a continuum of argument [math]\displaystyle{ \omega, }[/math] the result is called the Fourier transform.[upper-alpha 1]
For instance, consider the function:
- [math]\displaystyle{ f(t)= A_1 e^{i \omega_1 t}+A_2 e^{i \omega_2 t},\ \forall\ t \in \mathbb R,\ \omega_1 \gt 0,\ \omega_2 \gt 0. }[/math]
And:
- [math]\displaystyle{ \begin{align} \hat{f}(\omega) &= \int_{-\infty}^\infty [A_1 e^{i \omega_1 t}+A_2 e^{i \omega_2 t}] e^{-i \omega t} dt\\ &= \int_{-\infty}^\infty A_1 e^{i \omega_1 t} e^{-i \omega t} dt + \int_{-\infty}^\infty A_2 e^{i \omega_2 t} e^{-i \omega t} dt\\ &= \int_{-\infty}^\infty A_1 e^{i (\omega_1 -\omega) t}dt + \int_{-\infty}^\infty A_2 e^{i (\omega_2 -\omega) t} dt \end{align} }[/math]
Note that although most functions do not comprise infinite duration sinusoids, that idealization is a common simplification to facilitate understanding.
Looking at the first term of this result, when [math]\displaystyle{ \omega = \omega_1, }[/math] the negative frequency [math]\displaystyle{ -\omega_1 }[/math] cancels the positive frequency, leaving just the constant coefficient [math]\displaystyle{ A_1 }[/math] (because [math]\displaystyle{ e^{i 0 t} = e^0 = 1 }[/math]), which causes the infinite integral to diverge. At other values of [math]\displaystyle{ \omega }[/math] the residual oscillations cause the integral to converge to zero. This idealized Fourier transform is usually written as:
- [math]\displaystyle{ \hat{f}(\omega) = 2\pi A_1 \delta(\omega - \omega_1) + 2\pi A_2 \delta(\omega - \omega_2). }[/math]
For realistic durations, the divergences and convergences are less extreme, and smaller non-zero convergences (spectral leakage) appear at many other frequencies, but the concept of negative frequency still applies. Fourier's original formulation (the sine transform and the cosine transform) requires an integral for the cosine and another for the sine. And the resultant trigonometric expressions are often less tractable than complex exponential expressions. (see Analytic signal, Euler's formula § Relationship to trigonometry, and Phasor)
Sampling of positive and negative frequencies and aliasing
See also
Notes
- ↑ There are several forms of the Fourier transform. This is the non-unitary form in angular frequency of time
Further reading
- Positive and Negative Frequencies
- Lyons, Richard G. (Nov 11, 2010). Chapt 8.4. Understanding Digital Signal Processing (3rd ed.). Prentice Hall. 944 pgs. ISBN:0137027419.
- Lyons, Richard G. (Nov 2001). "Understanding Digital Signal Processing's Frequency Domain". https://www.researchgate.net/publication/261779218.
 |  |
