Radian

Short description: SI derived unit of angle

Radian
An arc of a circle with the same length as the radius of that circle subtends an angle of 1 radian. The circumference subtends an angle of 2π radians.
General information
Unit system	SI
Unit of	angle
Symbol	rad
Conversions
1 rad in ...	... is equal to ...
milliradians	1000 mrad
turns	1/2π turn
degrees	180/π° ≈ 57.296°
gradians	200/π grad ≈ 63.662g

The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless SI derived unit, defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as rad = m/m. Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing.

Definition

One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, [math]\displaystyle{ \theta = \frac{s}{r} }[/math], where θ is the subtended angle in radians, s is arc length, and r is radius. A right angle is exactly [math]\displaystyle{ \frac{\pi}{2} }[/math] radians.

The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, which is [math]\displaystyle{ \frac {2\pi r}{r} }[/math], or 2π. Thus, 2π radians is equal to 360 degrees.

The relation 2π rad = 360° can be derived using the formula for arc length, [math]\displaystyle{ \ell_{\text{arc}}=2\pi r\left(\tfrac{\theta}{360^{\circ}}\right) }[/math]. Since radian is the measure of an angle that is subtended by an arc of a length equal to the radius of the circle, [math]\displaystyle{ 1=2\pi\left(\tfrac{1\text{ rad}}{360^{\circ}}\right) }[/math]. This can be further simplified to [math]\displaystyle{ 1=\tfrac{2\pi\text{ rad}}{360^{\circ}} }[/math]. Multiplying both sides by 360° gives 360° = 2π rad.

Unit symbol

The International Bureau of Weights and Measures and International Organization for Standardization specify rad as the symbol for the radian. Alternative symbols that were in use in 1909 are ^c (the superscript letter c, for "circular measure"), the letter r, or a superscript ^R, but these variants are infrequently used, as they may be mistaken for a degree symbol (°) or a radius (r). Hence an angle of 1.2 radians would be written today as 1.2 rad; archaic notations could include 1.2 r, 1.2^rad, 1.2^c, or 1.2^R.

In mathematical writing, the symbol "rad" is often omitted. When quantifying an angle in the absence of any symbol, radians are assumed, and when degrees are meant, the degree sign ° is used.

Dimensional analysis

Plane angle may be defined as θ = s/r, where θ is the subtended angle in radians, s is arc length, and r is radius. One radian corresponds to the angle for which s = r, hence 1 radian = 1 m/m. However, rad is only to be used to express angles, not to express ratios of lengths in general. A similar calculation using the area of a circular sector θ = 2A/r² gives 1 radian as 1 m²/m². The key fact is that the radian is a dimensionless unit equal to 1. In SI 2019, the radian is defined accordingly as 1 rad = 1. It is a long-established practice in mathematics and across all areas of science to make use of rad = 1.

Giacomo Prando writes "the current state of affairs leads inevitably to ghostly appearances and disappearances of the radian in the dimensional analysis of physical equations". For example, an object hanging by a string from a pulley will rise or drop by y = rθ centimeters, where r is the radius of the pulley in centimeters and θ is the angle the pulley turns in radians. When multiplying r by θ the unit of radians disappears from the result. Similarly in the formula for the angular velocity of a rolling wheel, ω = v/r, radians appear in the units of ω but not on the right hand side. Anthony French calls this phenomenon "a perennial problem in the teaching of mechanics". Oberhofer says that the typical advice of ignoring radians during dimensional analysis and adding or removing radians in units according to convention and contextual knowledge is "pedagogically unsatisfying".

In 1993 the American Association of Physics Teachers Metric Committee specified that the radian should explicitly appear in quantities only when different numerical values would be obtained when other angle measures were used, such as in the quantities of angle measure (rad), angular speed (rad/s), angular acceleration (rad/s²), and torsional stiffness (N⋅m/rad), and not in the quantities of torque (N⋅m) and angular momentum (kg⋅m²/s).

At least a dozen scientists between 1936 and 2022 have made proposals to treat the radian as a base unit of measurement for a base quantity (and dimension) of "plane angle". Quincey's review of proposals outlines two classes of proposal. The first option changes the unit of a radius to meters per radian, but this is incompatible with dimensional analysis for the area of a circle, πr². The other option is to introduce a dimensional constant. According to Quincey this approach is "logically rigorous" compared to SI, but requires "the modification of many familiar mathematical and physical equations". A dimensional constant for angle is "rather strange" and the difficulty of modifying equations to add the dimensional constant is likely to preclude widespread use.

In particular, Quincey identifies Torrens' proposal to introduce a constant η equal to 1 inverse radian (1 rad⁻¹) in a fashion similar to the introduction of the constant ε₀. With this change the formula for the angle subtended at the center of a circle, s = rθ, is modified to become s = ηrθ, and the Taylor series for the sine of an angle θ becomes: [math]\displaystyle{ \operatorname{Sin} \theta = \sin_\text{rad} x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots = \eta \theta - \frac{(\eta \theta)^3}{3!} + \frac{(\eta \theta)^5}{5!} - \frac{(\eta \theta)^7}{7!} + \cdots , }[/math] where [math]\displaystyle{ x = \eta \theta = \theta/\text{rad} }[/math]. The capitalized function Sin is the "complete" function that takes an argument with a dimension of angle and is independent of the units expressed, while sin_rad is the traditional function on pure numbers which assumes its argument is in radians. [math]\displaystyle{ \operatorname{Sin} }[/math] can be denoted [math]\displaystyle{ \sin }[/math] if it is clear that the complete form is meant.

Current SI can be considered relative to this framework as a natural unit system where the equation η = 1 is assumed to hold, or similarly, 1 rad = 1. This radian convention allows the omission of η in mathematical formulas.

Defining radian as a base unit may be useful for software, where the disadvantage of longer equations is minimal. For example, the Boost units library defines angle units with a plane_angle dimension, and Mathematica's unit system similarly considers angles to have an angle dimension.

Conversions

Conversion of common angles

Turns	Radians	Degrees	Gradians, or gons
0	0	0°	0g
1/24	π/12	15°	16+2/3g
1/12	π/6	30°	33+1/3g
1/10	π/5	36°	40g
1/8	π/4	45°	50g
1/2π	1	c. 57.3°	c. 63.7g
1/6	π/3	60°	66+2/3g
1/5	2π/5	72°	80g
1/4	π/2	90°	100g
1/3	2π/3	120°	133+1/3g
2/5	4π/5	144°	160g
1/2	π	180°	200g
3/4	3π/2	270°	300g
1	2π	360°	400g

Between degrees

As stated, one radian is equal to [math]\displaystyle{ {180^\circ}/{\pi} }[/math]. Thus, to convert from radians to degrees, multiply by [math]\displaystyle{ {180^\circ}/{\pi} }[/math].

[math]\displaystyle{ \text{angle in degrees} = \text{angle in radians} \cdot \frac {180^\circ} {\pi} }[/math]

For example:

[math]\displaystyle{ 1 \text{ rad} = 1 \cdot \frac {180^\circ} {\pi} \approx 57.2958^\circ }[/math]

[math]\displaystyle{ 2.5 \text{ rad} = 2.5 \cdot \frac {180^\circ} {\pi} \approx 143.2394^\circ }[/math]

[math]\displaystyle{ \frac {\pi} {3} \text{ rad} = \frac {\pi} {3} \cdot \frac {180^\circ} {\pi} = 60^\circ }[/math]

Conversely, to convert from degrees to radians, multiply by [math]\displaystyle{ {\pi}/{180^\circ} }[/math].

[math]\displaystyle{ \text{angle in radians} = \text{angle in degrees} \cdot \frac {\pi} {180^\circ} }[/math]

For example:

[math]\displaystyle{ 1^\circ = 1^\circ \cdot \frac {\pi} {180^\circ} \approx 0.0175 \text{ rad} }[/math]

[math]\displaystyle{ 23^\circ = 23^\circ \cdot \frac {\pi} {180^\circ} \approx 0.4014 \text{ rad} }[/math]

Radians can be converted to turns (one turn is the angle corresponding to a revolution) by dividing the number of radians by 2π.

Between gradians

[math]\displaystyle{ 2\pi }[/math] radians equals one turn, which is by definition 400 gradians (400 gons or 400^g). To convert from radians to gradians multiply by [math]\displaystyle{ 200^\text{g}/\pi }[/math], and to convert from gradians to radians multiply by [math]\displaystyle{ \pi/200^\text{g} }[/math]. For example,

[math]\displaystyle{ 1.2 \text{ rad} = 1.2 \cdot \frac {200^\text{g}} {\pi} \approx 76.3944^\text{g} }[/math]

[math]\displaystyle{ 50^\text{g} = 50^\text{g} \cdot \frac {\pi} {200^\text{g}} \approx 0.7854 \text{ rad} }[/math]

Usage

Mathematics

Some common angles, measured in radians. All the large polygons in this diagram are regular polygons.

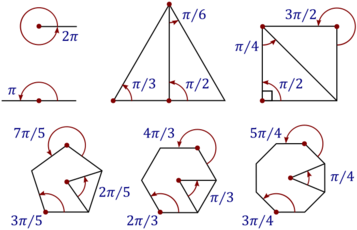
In calculus and most other branches of mathematics beyond practical geometry, angles are measured in radians. This is because radians have a mathematical naturalness that leads to a more elegant formulation of some important results.

Results in analysis involving trigonometric functions can be elegantly stated when the functions' arguments are expressed in radians. For example, the use of radians leads to the simple limit formula

[math]\displaystyle{ \lim_{h\rightarrow 0}\frac{\sin h}{h}=1, }[/math]

which is the basis of many other identities in mathematics, including

[math]\displaystyle{ \frac{d}{dx} \sin x = \cos x }[/math]

[math]\displaystyle{ \frac{d^2}{dx^2} \sin x = -\sin x. }[/math]

Because of these and other properties, the trigonometric functions appear in solutions to mathematical problems that are not obviously related to the functions' geometrical meanings (for example, the solutions to the differential equation [math]\displaystyle{ \tfrac{d^2 y}{dx^2} = -y }[/math], the evaluation of the integral [math]\displaystyle{ \textstyle\int \frac{dx}{1+x^2}, }[/math] and so on). In all such cases, it is found that the arguments to the functions are most naturally written in the form that corresponds, in geometrical contexts, to the radian measurement of angles.

The trigonometric functions also have simple and elegant series expansions when radians are used. For example, when x is in radians, the Taylor series for sin x becomes:

[math]\displaystyle{ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots . }[/math]

If x were expressed in degrees, then the series would contain messy factors involving powers of π/180: if x is the number of degrees, the number of radians is y = πx / 180, so

[math]\displaystyle{ \sin x_\mathrm{deg} = \sin y_\mathrm{rad} = \frac{\pi}{180} x - \left (\frac{\pi}{180} \right )^3\ \frac{x^3}{3!} + \left (\frac{\pi}{180} \right )^5\ \frac{x^5}{5!} - \left (\frac{\pi}{180} \right )^7\ \frac{x^7}{7!} + \cdots . }[/math]

In a similar spirit, mathematically important relationships between the sine and cosine functions and the exponential function (see, for example, Euler's formula) can be elegantly stated, when the functions' arguments are in radians (and messy otherwise).

Physics

The radian is widely used in physics when angular measurements are required. For example, angular velocity is typically expressed in the unit radian per second (rad/s). One revolution per second corresponds to 2π radians per second.

Similarly, the unit used for angular acceleration is often radian per second per second (rad/s²).

For the purpose of dimensional analysis, the units of angular velocity and angular acceleration are s⁻¹ and s⁻² respectively.

Likewise, the phase difference of two waves can also be expressed using the radian as the unit. For example, if the phase difference of two waves is (n⋅2π) radians with n is an integer, they are considered to be in phase, whilst if the phase difference of two waves is (n⋅2π + π) with n an integer, they are considered to be in antiphase.

Reciprocal radians or inverse radians (rad^-1) is involved in derived units such as meters per radian (for angular wavelength) or joule per radian (equivalent to newton-metre).

Prefixes and variants

Metric prefixes for submultiples are used with radians. A milliradian (mrad) is a thousandth of a radian (0.001 rad), i.e. 1 rad = 10³ mrad. There are 2π × 1000 milliradians (≈ 6283.185 mrad) in a circle. So a milliradian is just under 1/6283 of the angle subtended by a full circle. This unit of angular measurement of a circle is in common use by telescopic sight manufacturers using (stadiametric) rangefinding in reticles. The divergence of laser beams is also usually measured in milliradians.

The angular mil is an approximation of the milliradian used by NATO and other military organizations in gunnery and targeting. Each angular mil represents 1/6400 of a circle and is 15/8% or 1.875% smaller than the milliradian. For the small angles typically found in targeting work, the convenience of using the number 6400 in calculation outweighs the small mathematical errors it introduces. In the past, other gunnery systems have used different approximations to 1/2000π; for example Sweden used the 1/6300 streck and the USSR used 1/6000. Being based on the milliradian, the NATO mil subtends roughly 1 m at a range of 1000 m (at such small angles, the curvature is negligible).

Prefixes smaller than milli- are useful in measuring extremely small angles. Microradians (μrad, 10⁻⁶ rad) and nanoradians (nrad, 10⁻⁹ rad) are used in astronomy, and can also be used to measure the beam quality of lasers with ultra-low divergence. More common is the arc second, which is π/648,000 rad (around 4.8481 microradians).

SI multiples of radian (rad)

Submultiples				Multiples
Value	SI symbol	Name		Value	SI symbol	Name
10−1 rad	drad	deciradian		101 rad	darad	decaradian
10−2 rad	crad	centiradian		102 rad	hrad	hectoradian
10−3 rad	mrad	milliradian		103 rad	krad	kiloradian
10−6 rad	µrad	microradian		106 rad	Mrad	megaradian
10−9 rad	nrad	nanoradian		109 rad	Grad	gigaradian
10−12 rad	prad	picoradian		1012 rad	Trad	teraradian
10−15 rad	frad	femtoradian		1015 rad	Prad	petaradian
10−18 rad	arad	attoradian		1018 rad	Erad	exaradian
10−21 rad	zrad	zeptoradian		1021 rad	Zrad	zettaradian
10−24 rad	yrad	yoctoradian		1024 rad	Yrad	yottaradian

History

Pre-20th century

The idea of measuring angles by the length of the arc was in use by mathematicians quite early. For example, al-Kashi (c. 1400) used so-called diameter parts as units, where one diameter part was 1/60 radian. They also used sexagesimal subunits of the diameter part. Newton in 1672 spoke of "the angular quantity of a body's circular motion", but used it only as a relative measure to develop an astronomical algorithm.

The concept of the radian measure is normally credited to Roger Cotes, who died in 1716. By 1722, his cousin Robert Smith had collected and published Cotes' mathematical writings in a book, Harmonia mensurarum. In a chapter of editorial comments, Smith gave what is probably the first published calculation of one radian in degrees, citing a note of Cotes that has not survived. Smith described the radian in everything but name – "Now this number is equal to 180 degrees as the radius of a circle to the semicircumference, this is as 1 to 3.141592653589" –, and recognized its naturalness as a unit of angular measure.

In 1765, Leonhard Euler implicitly adopted the radian as a unit of angle. Specifically, Euler defined angular velocity as "The angular speed in rotational motion is the speed of that point, the distance of which from the axis of gyration is expressed by one." Euler was probably the first to adopt this convention, referred to as the radian convention, which gives the simple formula for angular velocity ω = v/r. As discussed in § Dimensional analysis, the radian convention has been widely adopted, and other conventions have the drawback of requiring a dimensional constant, for example ω = v/(ηr).

Prior to the term radian becoming widespread, the unit was commonly called circular measure of an angle. The term radian first appeared in print on 5 June 1873, in examination questions set by James Thomson (brother of Lord Kelvin) at Queen's College, Belfast. He had used the term as early as 1871, while in 1869, Thomas Muir, then of the University of St Andrews, vacillated between the terms rad, radial, and radian. In 1874, after a consultation with James Thomson, Muir adopted radian. The name radian was not universally adopted for some time after this. Longmans' School Trigonometry still called the radian circular measure when published in 1890.

In 1893 Alexander Macfarlane wrote "the true analytical argument for the circular ratios is not the ratio of the arc to the radius, but the ratio of twice the area of a sector to the square on the radius." For some reason the paper was withdrawn from the published proceedings of mathematical congress held in connection with World's Columbian Exposition in Chicago (acknowledged at page 167), and privately published in his Papers on Space Analysis (1894). Macfarlane reached this idea or ratios of areas while considering the basis for hyperbolic angle which is analogously defined.

As a SI unit

As Paul Quincey et al. writes, "the status of angles within the International System of Units (SI) has long been a source of controversy and confusion." In 1960, the CGPM established the SI and the radian was classified as a "supplementary unit" along with the steradian. This special class was officially regarded "either as base units or as derived units", as the CGPM could not reach a decision on whether the radian was a base unit or a derived unit. Richard Nelson writes "This ambiguity [in the classification of the supplemental units] prompted a spirited discussion over their proper interpretation." In May 1980 the Consultative Committee for Units (CCU) considered a proposal for making radians an SI base unit, using a constant α₀ = 1 rad, but turned it down to avoid an upheaval to current practice.

In October 1980 the CGPM decided that supplementary units were dimensionless derived units for which the CGPM allowed the freedom of using them or not using them in expressions for SI derived units, on the basis that "[no formalism] exists which is at the same time coherent and convenient and in which the quantities plane angle and solid angle might be considered as base quantities" and that "[the possibility of treating the radian and steradian as SI base units] compromises the internal coherence of the SI based on only seven base units". In 1995 the CGPM eliminated the class of supplementary units and defined the radian and the steradian as "dimensionless derived units, the names and symbols of which may, but need not, be used in expressions for other SI derived units, as is convenient". Mikhail Kalinin writing in 2019 has criticized the 1980 CGPM decision as "unfounded" and says that the 1995 CGPM decision used inconsistent arguments and introduced "numerous discrepancies, inconsistencies, and contradictions in the wordings of the SI".

At the 2013 meeting of the CCU, Peter Mohr gave a presentation on alleged inconsistencies arising from defining the radian as a dimensionless unit rather than a base unit. CCU President Ian M. Mills declared this to be a "formidable problem" and the CCU Working Group on Angles and Dimensionless Quantities in the SI was established. (As of 2021) but did not reach a consensus. A small number of members argued strongly that the radian should be a base unit, but the majority felt the status quo was acceptable or that the change would cause more problems than it would solve. A task group was established to "review the historical use of SI supplementary units and consider whether reintroduction would be of benefit", among other activities.

See also

• Angular frequency
• Minute and second of arc
• Steradian, a higher-dimensional analog of the radian which measures solid angle
• Trigonometry

References

• International Bureau of Weights and Measures (20 May 2019), The International System of Units (SI) (9th ed.), ISBN 978-92-822-2272-0, https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf#page=37 
• Brinsmade, J. B. (December 1936). "Plane and Solid Angles. Their Pedagogic Value When Introduced Explicitly". American Journal of Physics 4 (4): 175–179. doi:10.1119/1.1999110. Bibcode: 1936AmJPh...4..175B. 
• Romain, Jacques E. (July 1962). "Angle as a fourth fundamental quantity". Journal of Research of the National Bureau of Standards Section B 66B (3): 97. doi:10.6028/jres.066B.012. 
• Eder, W E (January 1982). "A Viewpoint on the Quantity "Plane Angle"". Metrologia 18 (1): 1–12. doi:10.1088/0026-1394/18/1/002. Bibcode: 1982Metro..18....1E. 
• Torrens, A B (1 January 1986). "On Angles and Angular Quantities". Metrologia 22 (1): 1–7. doi:10.1088/0026-1394/22/1/002. Bibcode: 1986Metro..22....1T. 
• Brownstein, K. R. (July 1997). "Angles—Let's treat them squarely". American Journal of Physics 65 (7): 605–614. doi:10.1119/1.18616. Bibcode: 1997AmJPh..65..605B. 
• Lévy-Leblond, Jean-Marc (September 1998). "Dimensional angles and universal constants". American Journal of Physics 66 (9): 814–815. doi:10.1119/1.18964. Bibcode: 1998AmJPh..66..814L. https://www.researchgate.net/publication/253371022. 
• Foster, Marcus P (1 December 2010). "The next 50 years of the SI: a review of the opportunities for the e-Science age". Metrologia 47 (6): R41–R51. doi:10.1088/0026-1394/47/6/R01. https://publications.csiro.au/rpr/download?pid=csiro:EP11794&dsid=DS4. 
• Mohr, Peter J; Phillips, William D (1 February 2015). "Dimensionless units in the SI". Metrologia 52 (1): 40–47. doi:10.1088/0026-1394/52/1/40. Bibcode: 2015Metro..52...40M. 
• Quincey, Paul (1 April 2016). "The range of options for handling plane angle and solid angle within a system of units". Metrologia 53 (2): 840–845. doi:10.1088/0026-1394/53/2/840. Bibcode: 2016Metro..53..840Q. 
• Mills, Ian (1 June 2016). "On the units radian and cycle for the quantity plane angle". Metrologia 53 (3): 991–997. doi:10.1088/0026-1394/53/3/991. Bibcode: 2016Metro..53..991M. 
• Quincey, Paul (1 October 2021). "Angles in the SI: a detailed proposal for solving the problem". Metrologia 58 (5): 053002. doi:10.1088/1681-7575/ac023f. Bibcode: 2021Metro..58e3002Q. 
• Leonard, B P (1 October 2021). "Proposal for the dimensionally consistent treatment of angle and solid angle by the International System of Units (SI)". Metrologia 58 (5): 052001. doi:10.1088/1681-7575/abe0fc. Bibcode: 2021Metro..58e2001L. 
• Mohr, Peter J; Shirley, Eric L; Phillips, William D; Trott, Michael (23 June 2022). "On the dimension of angles and their units". Metrologia 59 (5): 053001. doi:10.1088/1681-7575/ac7bc2. Bibcode: 2022Metro..59e3001M.