Nodal decomposition
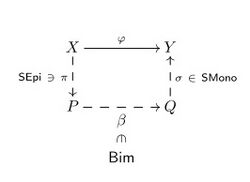
In category theory, an abstract mathematical discipline, a nodal decomposition[1] of a morphism [math]\displaystyle{ \varphi:X\to Y }[/math] is a representation of [math]\displaystyle{ \varphi }[/math] as a product [math]\displaystyle{ \varphi=\sigma\circ\beta\circ\pi }[/math], where [math]\displaystyle{ \pi }[/math] is a strong epimorphism,[2][3][4] [math]\displaystyle{ \beta }[/math] a bimorphism, and [math]\displaystyle{ \sigma }[/math] a strong monomorphism.[5][3][4]
Uniqueness and notations
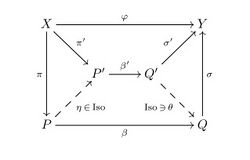
If it exists, the nodal decomposition is unique up to an isomorphism in the following sense: for any two nodal decompositions [math]\displaystyle{ \varphi=\sigma\circ\beta\circ\pi }[/math] and [math]\displaystyle{ \varphi=\sigma'\circ\beta'\circ\pi' }[/math] there exist isomorphisms [math]\displaystyle{ \eta }[/math] and [math]\displaystyle{ \theta }[/math] such that
- [math]\displaystyle{ \pi'=\eta\circ\pi, }[/math]
- [math]\displaystyle{ \beta=\theta\circ\beta'\circ\eta, }[/math]
- [math]\displaystyle{ \sigma'=\sigma\circ\theta. }[/math]
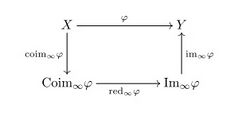
This property justifies some special notations for the elements of the nodal decomposition:
- [math]\displaystyle{ \begin{align} & \pi=\operatorname{coim}_\infty \varphi, && P=\operatorname{Coim}_\infty \varphi,\\ & \beta=\operatorname{red}_\infty \varphi, && \\ & \sigma=\operatorname{im}_\infty \varphi, && Q=\operatorname{Im}_\infty \varphi, \end{align} }[/math]
– here [math]\displaystyle{ \operatorname{coim}_\infty \varphi }[/math] and [math]\displaystyle{ \operatorname{Coim}_\infty \varphi }[/math] are called the nodal coimage of [math]\displaystyle{ \varphi }[/math], [math]\displaystyle{ \operatorname{im}_\infty \varphi }[/math] and [math]\displaystyle{ \operatorname{Im}_\infty \varphi }[/math] the nodal image of [math]\displaystyle{ \varphi }[/math], and [math]\displaystyle{ \operatorname{red}_\infty \varphi }[/math] the nodal reduced part of [math]\displaystyle{ \varphi }[/math].
In these notations the nodal decomposition takes the form
- [math]\displaystyle{ \varphi=\operatorname{im}_\infty \varphi\circ\operatorname{red}_\infty \varphi \circ \operatorname{coim}_\infty \varphi. }[/math]
Connection with the basic decomposition in pre-abelian categories
In a pre-abelian category [math]\displaystyle{ {\mathcal K} }[/math] each morphism [math]\displaystyle{ \varphi }[/math] has a standard decomposition
- [math]\displaystyle{ \varphi=\operatorname{im} \varphi\circ\operatorname{red} \varphi\circ\operatorname{coim} \varphi }[/math],
called the basic decomposition (here [math]\displaystyle{ \operatorname{im} \varphi=\ker(\operatorname{coker} \varphi) }[/math], [math]\displaystyle{ \operatorname{coim} \varphi=\operatorname{coker}(\ker\varphi) }[/math], and [math]\displaystyle{ \operatorname{red} \varphi }[/math] are respectively the image, the coimage and the reduced part of the morphism [math]\displaystyle{ \varphi }[/math]).
If a morphism [math]\displaystyle{ \varphi }[/math] in a pre-abelian category [math]\displaystyle{ {\mathcal K} }[/math] has a nodal decomposition, then there exist morphisms [math]\displaystyle{ \eta }[/math] and [math]\displaystyle{ \theta }[/math] which (being not necessarily isomorphisms) connect the nodal decomposition with the basic decomposition by the following identities:
- [math]\displaystyle{ \operatorname{coim}_\infty \varphi=\eta\circ\operatorname{coim} \varphi, }[/math]
- [math]\displaystyle{ \operatorname{red} \varphi=\theta\circ\operatorname{red}_\infty \varphi\circ\eta, }[/math]
- [math]\displaystyle{ \operatorname{im}_\infty \varphi=\operatorname{im} \varphi\circ\theta. }[/math]
Categories with nodal decomposition
A category [math]\displaystyle{ {\mathcal K} }[/math] is called a category with nodal decomposition[1] if each morphism [math]\displaystyle{ \varphi }[/math] has a nodal decomposition in [math]\displaystyle{ {\mathcal K} }[/math]. This property plays an important role in constructing envelopes and refinements in [math]\displaystyle{ {\mathcal K} }[/math].
In an abelian category [math]\displaystyle{ {\mathcal K} }[/math] the basic decomposition
- [math]\displaystyle{ \varphi=\operatorname{im} \varphi\circ\operatorname{red} \varphi\circ\operatorname{coim} \varphi }[/math]
is always nodal. As a corollary, all abelian categories have nodal decomposition.
If a pre-abelian category [math]\displaystyle{ {\mathcal K} }[/math] is linearly complete,[6] well-powered in strong monomorphisms[7] and co-well-powered in strong epimorphisms,[8] then [math]\displaystyle{ {\mathcal K} }[/math] has nodal decomposition.[9]
More generally, suppose a category [math]\displaystyle{ {\mathcal K} }[/math] is linearly complete,[6] well-powered in strong monomorphisms,[7] co-well-powered in strong epimorphisms,[8] and in addition strong epimorphisms discern monomorphisms[10] in [math]\displaystyle{ {\mathcal K} }[/math], and, dually, strong monomorphisms discern epimorphisms[11] in [math]\displaystyle{ {\mathcal K} }[/math], then [math]\displaystyle{ {\mathcal K} }[/math] has nodal decomposition.[12]
The category Ste of stereotype spaces (being non-abelian) has nodal decomposition,[13] as well as the (non-additive) category SteAlg of stereotype algebras .[14]
Notes
- ↑ 1.0 1.1 Akbarov 2016, p. 28.
- ↑ An epimorphism [math]\displaystyle{ \varepsilon:A\to B }[/math] is said to be strong, if for any monomorphism [math]\displaystyle{ \mu:C\to D }[/math] and for any morphisms [math]\displaystyle{ \alpha:A\to C }[/math] and [math]\displaystyle{ \beta:B\to D }[/math] such that [math]\displaystyle{ \beta\circ\varepsilon=\mu\circ\alpha }[/math] there exists a morphism [math]\displaystyle{ \delta:B\to C }[/math], such that [math]\displaystyle{ \delta\circ\varepsilon=\alpha }[/math] and [math]\displaystyle{ \mu\circ\delta=\beta }[/math]. thumb
- ↑ 3.0 3.1 Borceux 1994.
- ↑ 4.0 4.1 Tsalenko 1974.
- ↑ A monomorphism [math]\displaystyle{ \mu:C\to D }[/math] is said to be strong, if for any epimorphism [math]\displaystyle{ \varepsilon:A\to B }[/math] and for any morphisms [math]\displaystyle{ \alpha:A\to C }[/math] and [math]\displaystyle{ \beta:B\to D }[/math] such that [math]\displaystyle{ \beta\circ\varepsilon=\mu\circ\alpha }[/math] there exists a morphism [math]\displaystyle{ \delta:B\to C }[/math], such that [math]\displaystyle{ \delta\circ\varepsilon=\alpha }[/math] and [math]\displaystyle{ \mu\circ\delta=\beta }[/math]
- ↑ 6.0 6.1 A category [math]\displaystyle{ {\mathcal K} }[/math] is said to be linearly complete, if any functor from a linearly ordered set into [math]\displaystyle{ {\mathcal K} }[/math] has direct and inverse limits.
- ↑ 7.0 7.1 A category [math]\displaystyle{ {\mathcal K} }[/math] is said to be well-powered in strong monomorphisms, if for each object [math]\displaystyle{ X }[/math] the category [math]\displaystyle{ \operatorname{SMono}(X) }[/math] of all strong monomorphisms into [math]\displaystyle{ X }[/math] is skeletally small (i.e. has a skeleton which is a set).
- ↑ 8.0 8.1 A category [math]\displaystyle{ {\mathcal K} }[/math] is said to be co-well-powered in strong epimorphisms, if for each object [math]\displaystyle{ X }[/math] the category [math]\displaystyle{ \operatorname{SEpi}(X) }[/math] of all strong epimorphisms from [math]\displaystyle{ X }[/math] is skeletally small (i.e. has a skeleton which is a set).
- ↑ Akbarov 2016, p. 37.
- ↑ It is said that strong epimorphisms discern monomorphisms in a category [math]\displaystyle{ {\mathcal K} }[/math], if each morphism [math]\displaystyle{ \mu }[/math], which is not a monomorphism, can be represented as a composition [math]\displaystyle{ \mu=\mu'\circ\varepsilon }[/math], where [math]\displaystyle{ \varepsilon }[/math] is a strong epimorphism which is not an isomorphism.
- ↑ It is said that strong monomorphisms discern epimorphisms in a category [math]\displaystyle{ {\mathcal K} }[/math], if each morphism [math]\displaystyle{ \varepsilon }[/math], which is not an epimorphism, can be represented as a composition [math]\displaystyle{ \varepsilon=\mu\circ\varepsilon' }[/math], where [math]\displaystyle{ \mu }[/math] is a strong monomorphism which is not an isomorphism.
- ↑ Akbarov 2016, p. 31.
- ↑ Akbarov 2016, p. 142.
- ↑ Akbarov 2016, p. 164.
References
- Borceux, F. (1994). Handbook of Categorical Algebra 1. Basic Category Theory. Cambridge University Press. ISBN 978-0521061193. https://archive.org/details/handbookofcatego0000borc.
- Tsalenko, M.S.; Shulgeifer, E.G. (1974). Foundations of category theory. Nauka.
- Akbarov, S.S. (2016). "Envelopes and refinements in categories, with applications to functional analysis". Dissertationes Mathematicae 513: 1–188. doi:10.4064/dm702-12-2015. https://www.impan.pl/en/publishing-house/journals-and-series/dissertationes-mathematicae/all/513.
 |  |
