Nondeterministic constraint logic

In theoretical computer science, nondeterministic constraint logic is a combinatorial system in which an orientation is given to the edges of a weighted undirected graph, subject to certain constraints. One can change this orientation by steps in which a single edge is reversed, subject to the same constraints. The constraint logic problem and its variants have been proven to be PSPACE-complete to determine whether there exists a sequence of moves that reverses a specified edge and are very useful to show various games and puzzles are PSPACE-hard or PSPACE-complete.

This is a form of reversible logic in that each sequence of edge orientation changes can be undone. The hardness of this problem has been used to prove that many games and puzzles have high game complexity.

Constraint graphs

An AND gate in constraint logic. As the minimum in-degree of the node is 2, the top edge can be out if and only if the two bottom edges are in.

Example of a constraint graph.

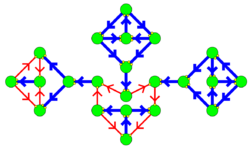
In the simplest version of nondeterministic constraint logic, each edge of an undirected graph has weight either one or two. (The weights may also be represented graphically by drawing edges of weight one as red and edges of weight two as blue.) The graph is required to be a cubic graph: each vertex is incident to three edges, and additionally each vertex should be incident to an even number of red edges.

The edges are required to be oriented in such a way that at least two units of weight are oriented towards each vertex: there must be either at least one incoming blue edge, or at least two incoming red edges. An orientation can change by steps in which a single edge is reversed, respecting these constraints.

More general forms of nondeterministic constraint logic allow a greater variety of edge weights, more edges per vertex, and different thresholds for how much incoming weight each vertex must have. A graph with a system of edge weights and vertex thresholds is called a constraint graph. The restricted case where the edge weights are all one or two, the vertices require two units of incoming weight, and the vertices all have three incident edges with an even number of red edges, are called and/or constraint graphs.

The reason for the name and/or constraint graphs is that the two possible types of vertex in an and/or constraint graph behave in some ways like an AND gate and OR gate in Boolean logic. A vertex with two red edges and one blue edge behaves like an AND gate in that it requires both red edges to point inwards before the blue edge can be made to point outwards. A vertex with three blue edges behaves like an OR gate, with two of its edges designated as inputs and the third as an output, in that it requires at least one input edge to point inwards before the output edge can be made to point outwards.

Typically, constraint logic problems are defined around finding valid configurations of constraint graphs. Constraint graphs are undirected graphs with two types of edges:

• red edges with weight [math]\displaystyle{ 1 }[/math]
• blue edges with weight [math]\displaystyle{ 2 }[/math]

We use constraint graphs as computation models, where we think of the entire graph as a machine. A configuration of the machine consists of the graph along with a specific orientation of its edges. We call a configuration valid, if it satisfies the inflow constraint: each vertex must have an incoming weight of at least [math]\displaystyle{ 2 }[/math]. In other words, the sum of the weights of the edges that enter a given vertex must be at least [math]\displaystyle{ 2 }[/math] more than the sum of the weights of the edges that exit the vertex.

We also define a move in a constraint graph to be the action of reversing the orientation of an edge, such that the resulting configuration is still valid.

Formal definition of the Constraint logic problem

Suppose we are given a constraint graph, a starting configuration and an ending configuration. This problem asks if there exists a sequence of valid moves that move it from the starting configuration to the ending configuration This problem is PSPACE-Complete for 3-regular or max-degree 3 graphs. The reduction follows from QSAT and is outlined below.

Variants

Planar Non-Deterministic Constraint Logic

The above problem is PSPACE-Complete even if the constraint graph is planar, i.e. no the graph can be drawn in a way such that no two edges cross each other. This reduction follows from Planar QSAT.

Edge Reversal

This problem is a special case of the previous one. It asks, given a constraint graph, if it is possible to reverse a specified edge by a sequence of valid moves. Note that this could be done by a sequence of valid moves so long as the last valid move reverses the desired edge. This problem has also been proven to be PSPACE-Complete for 3-regular or max-degree 3 graphs.

Constraint Graph Satisfaction

This problem asks if there exists an orientation of the edges that satisfies the inflow constraints given an undirected graph [math]\displaystyle{ G }[/math]. This problem has been proven to be NP-Complete.

Hard problems

The following problems, on and/or constraint graphs and their orientations, are PSPACE-complete:

• Given an orientation and a specified edge e, testing whether there is a sequence of steps from the given orientation that eventually reverses edge e.
• Testing whether one orientation can be changed into another one by a sequence of steps.
• Given two edges e and f with specified directions, testing whether there are two orientations for the whole graph, one having the specified direction on e and the other having the specified direction on f, that can be transformed into each other by a sequence of steps.

The proof that these problems are hard involves a reduction from quantified Boolean formulas, based on the logical interpretation of and/or constraint graphs. It requires additional gadgets for simulating quantifiers and for converting signals carried on red edges into signals carried on blue edges (or vice versa), which can all be accomplished by combinations of and-vertices and or-vertices.

These problems remain PSPACE-complete even for and/or constraint graphs that form planar graphs. The proof of this involves the construction of crossover gadgets that allow two independent signals to cross each other. It is also possible to impose an additional restriction, while preserving the hardness of these problems: each vertex with three blue edges can be required to be part of a triangle with a red edge. Such a vertex is called a protected or, and it has the property that (in any valid orientation of the whole graph) it is not possible for both of the blue edges in the triangle to be directed inwards. This restriction makes it easier to simulate these vertices in hardness reductions for other problems. Additionally, the constraint graphs can be required to have bounded bandwidth, and the problems on them will still remain PSPACE-complete.

Proof of PSPACE-hardness

The reduction follows from QSAT. In order to embed a QSAT formula, we need to create AND, OR, NOT, UNIVERSAL, EXISTENTIAL, and Converter (to change color) gadgets in the constraint graph. The idea goes as follows:

• An AND vertex is a vertex such that it has two incident red edges (inputs) and one blue incident edge (output).
• An OR vertex is a vertex such that it has three incident blue edges (two inputs, one output).

The other gadgets can also be created in this manner. The full construction is available in Erik Demaine's website. The full construction is also explained in an interactive way.

Applications

The original applications of nondeterministic constraint logic used it to prove the PSPACE-completeness of sliding block puzzles such as Rush Hour and Sokoban. To do so, one needs only to show how to simulate edges and edge orientations, and vertices, and protected or vertices in these puzzles.

Nondeterministic constraint logic has also been used to prove the hardness of reconfiguration versions of classical graph optimization problems including the independent set, vertex cover, and dominating set, on planar graphs of bounded bandwidth. In these problems, one must change one solution to the given problem into another, by moving one vertex at a time into or out of the solution set while maintaining the property that at all times the remaining vertices form a solution.

Reconfiguration 3SAT

Given a 3-CNF formula and two satisfying assignments, this problem asks whether it is possible find a sequence of steps that take us from one assignment to the others, where in each step we are allowed to flip the value of a variable. This problem can be shown PSPACE-complete via a reduction from the Non-deterministic Constraint Logic problem.

Sliding-Block Puzzles

This problem asks whether we can reach a desired configuration in a sliding block puzzle given an initial configuration of the blocks. This problem is PSPACE-complete, even if the rectangles are dominoes.

Rush Hour

This problem asks whether we can reach the victory condition of rush hour puzzle given an initial configuration. This problem is PSPACE-complete, even if the blocks have size [math]\displaystyle{ 1\times 2 }[/math].

Dynamic Map Labeling

Given a static map, this problem asks whether there is a smooth dynamic labeling. This problem is also PSPACE-complete.