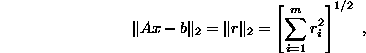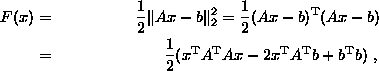Normal equations
We consider the problem 
, where A is an (m,n) matrix with 
, rank(A) = n, b is an (m,1) vector, and x is the (n,1) vector to be determined.
The sign 
stands for the least squares approximation, i.e. a minimization of the norm of the residual r = Ax - b
or the square
i.e. a differentiable function of x. The necessary condition for a minimum is:
These equations are called the normal equations , which become in our case:
The solution 
is usually computed with the following algorithm:
First (the lower triangular portion of) the symmetric matrix 
is computed, then its Cholesky decomposition 
. Thereafter one solves 
for y and finally x is computed from 
.
Unfortunately is often ill-conditioned and strongly influenced by roundoff errors (see Golub89). Other methods which do not compute ATA and solve directly are QR decomposition and singular value decomposition.
 |
