North east down
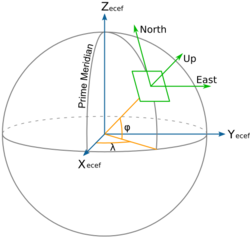
North east down (NED), also known as local tangent plane (LTP), is a geographical coordinate system for representing state vectors that is commonly used in aviation. It consists of three numbers: one represents the position along the northern axis, one along the eastern axis, and one represents vertical position. Down is chosen as opposed to up in order to comply with the right-hand rule. The origin of this coordinate system is usually chosen to be a point on the surface of the geoid below the aircraft's center of gravity. However, care must be taken since, if the aircraft is accelerating (turning or accelerating linearly), then the NED coordinates are no longer inertial coordinates.[1]
NED coordinates are similar to ECEF in that they're Cartesian, however they can be more convenient due to the relatively small numbers involved, and also because of the intuitive axes. NED and ECEF coordinates can be related with the following formula:[2]
- [math]\displaystyle{ \mathbf p_{\mathrm{NED}} = R^T (\mathbf p_{\mathrm{ECEF}} - \mathbf p_{\mathrm{Ref}}) }[/math]
where [math]\displaystyle{ \mathbf p_{\mathrm{NED}} }[/math] is a 3D position in a NED system, [math]\displaystyle{ \mathbf p_{\mathrm{ECEF}} }[/math] is the corresponding ECEF position, [math]\displaystyle{ \mathbf p_{\mathrm{Ref}} }[/math] is the reference ECEF position (where the local tangent plane originates), and [math]\displaystyle{ R }[/math] is a rotation matrix whose columns are the north, east, and down axes. [math]\displaystyle{ R }[/math] may be defined conveniently from the latitude [math]\displaystyle{ \phi }[/math] and longitude [math]\displaystyle{ \lambda }[/math] corresponding to [math]\displaystyle{ \mathbf p_{\mathrm{Ref}} }[/math]:
- [math]\displaystyle{ R = \begin{bmatrix} -\sin(\phi) \cos(\lambda) & -\sin(\lambda) & -\cos(\phi) \cos(\lambda) \\ -\sin(\phi) \sin(\lambda) & \cos(\lambda) & -\cos(\phi) \sin(\lambda) \\ \cos(\phi) & 0 & -\sin(\phi) \end{bmatrix} }[/math]
See also
- East north up
- Axes conventions
- Geodetic system
References
- ↑ Cai, Guowei; Chen, Ben M.; Lee, Tong Heng (2011). Unmanned Rotorcraft Systems. Springer. pp. 27. ISBN 978-0-85729-634-4.
- ↑ Cai, Guowei; Chen, Ben M.; Lee, Tong Heng (2011). Unmanned Rotorcraft Systems. Springer. pp. 32. ISBN 978-0-85729-634-4.