Null distribution
In statistical hypothesis testing, the null distribution is the probability distribution of the test statistic when the null hypothesis is true.[1] For example, in an F-test, the null distribution is an F-distribution.[2] Null distribution is a tool scientists often use when conducting experiments. The null distribution is the distribution of two sets of data under a null hypothesis. If the results of the two sets of data are not outside the parameters of the expected results, then the null hypothesis is said to be true.
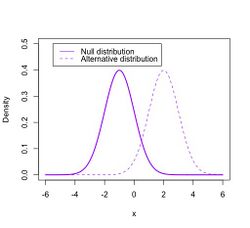
Examples of application
The null hypothesis is often a part of an experiment. The null hypothesis tries to show that among two sets of data, there is no statistical difference between the results of doing one thing as opposed to doing a different thing. For an example of this, a scientist might be trying to prove that people who walk two miles a day have healthier hearts than people who walk less than two miles a day. The scientist would use the null hypothesis to test the health of the hearts of people who walked two miles a day against the health of the hearts of the people who walked less than two miles a day. If there was no difference between their heart rate, then the scientist would be able to say that the test statistics would follow the null distribution. Then the scientists could determine that if there was significant difference that means the test follows the alternative distribution.
Obtaining the null distribution
In the procedure of hypothesis testing, one needs to form the joint distribution of test statistics to conduct the test and control type I errors. However, the true distribution is often unknown and a proper null distribution ought to be used to represent the data. For example, one sample and two samples tests of means can use t statistics which have Gaussian null distribution, while F statistics, testing k groups of population means, which have Gaussian quadratic form the null distribution.[3] The null distribution is defined as the asymptotic distributions of null quantile-transformed test statistics, based on marginal null distribution.[4] During practice, the test statistics of the null distribution is often unknown, since it relies on the unknown data generating distribution. Resampling procedures, such as non-parametric or model-based bootstrap, can provide consistent estimators for the null distributions. Improper choice of the null distribution poses significant influence on type I error and power properties in the testing process. Another approach to obtain the test statistics null distribution is to use the data of generating null distribution estimation.
Null distribution with large sample size
The null distribution plays a crucial role in large scale testing. Large sample size allows us to implement a more realistic empirical null distribution. One can generate the empirical null using an MLE fitting algorithm.[5] Under a Bayesian framework, the large-scale studies allow the null distribution to be put into a probabilistic context with its non-null counterparts. When sample size n is large, like over 10,000, the empirical nulls utilize a study's own data to estimate an appropriate null distribution. The important assumption is that due to the large proportion of null cases ( > 0.9), the data can show the null distribution itself. The theoretical null may fail in some cases, which is not completely wrong but needs adjustment accordingly. In the large-scale data sets, it is easy to find the deviations of data from the ideal mathematical framework, e.g., independent and identically distributed (i.i.d.) samples. In addition, the correlation across sampling units and unobserved covariates may lead to wrong theoretical null distribution.[6] Permutation methods are frequently used in multiple testing to obtain an empirical null distribution generated from data. Empirical null methods were introduced with the central matching algorithm in Efron's paper.[7]
Several points should be considered using permutation method. Permutation methods are not suitable for correlated sampling units, since the sampling process of permutation implies independence and requires i.i.d. assumptions. Furthermore, literature showed that the permutation distribution converges to N(0,1) quickly as n becomes large. In some cases, permutation techniques and empirical methods can be combined by using permutation null replace N(0,1) in the empirical algorithm.[8]
References
- ↑ Staley, Kent W. An Introduction to the Philosophy of Science. 2014. p. 142. ISBN 9780521112499.
- ↑ Jackson, Sally Ann. Random Factors in ANOVA. 1994. pp. 38. ISBN 9780803950900.
- ↑ Dudoit, S., and M. J. Van Der Laan. "Multiple testing procedures with applications to genomics. 2008."
- ↑ Van Der Laan, Mark J., and Alan E. Hubbard. "Quantile-function based null distribution in resampling based multiple testing." Statistical Applications in Genetics and Molecular Biology 5.1 (2006): 1199.
- ↑ Efron, Bradley, and Trevor Hastie. Computer Age Statistical Inference. Cambridge University Press, 2016.
- ↑ Efron, Bradley. Large-scale inference: empirical Bayes methods for estimation, testing, and prediction. Cambridge University Press, 2012.
- ↑ Efron, Bradley. "Large-scale simultaneous hypothesis testing: the choice of a null hypothesis." Journal of the American Statistical Association 99.465 (2004): 96-104.
- ↑ Efron, Bradley. Large-scale inference: empirical Bayes methods for estimation, testing, and prediction. Cambridge University Press, 2012.
 |

